Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 191
A escora tem seção transversal quadrada a por a e está sujeita ao momento fletor aplicado ao um ângulo como mostra a figura. Determine a tensão de flexão máxima em termos de , e . Qual ângulo resultará na maior tensão de flexão na escora? Especifique a orientação do eixo neutro para este caso.
Passo 1
Primeiro, vamos fazer o DCL:
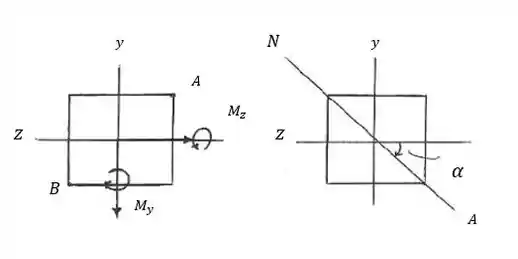
Passo 2
Com isso, vamos calcular o momento de inercia, os momentos e assim calcularmos a tensão:
Para
Para
Logo:
Passo 3
Por fim, para que a tensão seja máxima sua derivada em função de de ser igual a 0:
Portanto, para que ,
E para o coeficiente, temos:
Resposta
Exercícios de Livros Relacionados
Resolver o P r o b .4 . 13 2 , considerando que as deformações medidas são: ε A = + 35.10 - 6 m m m m eε B = - 450.10 - 6 m m m m
Resolver o P r o b .4 . 130 , considerando que as deformações medidas são: ε A = + 175μ eε B = - 50μ
O momento M é aplicado a uma viga de seção transversal mostrada, em um plano formado um ângulo β com a vertical. Determinar:A tensão no ponto A;A tensão no ponto B;O ângulo que a linha neutra forma co
O momento M é aplicado a uma viga de seção transversal mostrada, em um plano formado um ângulo β com a vertical. Determinar:A tensão no ponto A;A tensão no ponto B;O ângulo que a linha neutra forma co
O momento M é aplicado a uma viga de seção transversal mostrada, em um plano formado um ângulo β com a vertical. Determinar:A tensão no ponto A;A tensão no ponto B;O ângulo que a linha neutra forma co