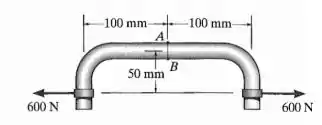
A haste curva tem diâmetro de 15 mm e está sujeita à força de 600 N. Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvidas no ponto A e no ponto B. Mostre os resultados em elementos localizados nesses pontos.
Passo 1
Fala! Primeiro a gente vai achar as tensões no plano e depois achar as principais, beleza?
Vamos começar calculando os esforços atuantes na seção. Só partir nosso elemento na seção , escolher só uma das metades, posicionar as componentes dos esforços na seção e usar as equações de equilíbrio para achar e .
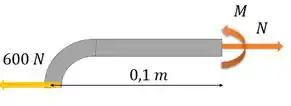
Passo 2
vai causar esforço normal de tração nos dois pontos. E momento vai causar tração em e compressão em (tensão negativa).
Os dois pontos distam do eixo neutro.
Logo, as tensões em A e B serão:
Passo 3
Logo, podemos calcular a tensão média e o raio do círculo de Mohr para A:
Como no caso em que calculamos não há cisalhamento, esse já seria o plano principal de tensões, assim:
Sabendo que o plano de tensões principal e o plano de cisalhamento máximo ocorrem a uma diferença de rotação de , nossos elementos ficam:
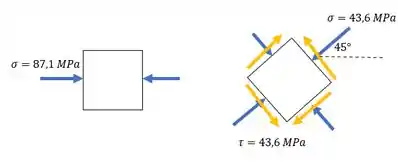
Repara que a orientação é no sentido anti-horário. A gente percebe isso ao montar o círculo de Mohr. Para chegar no estado de cisalhamento máximo, precisamos girar nesse sentido.
Passo 4
Já para B:
Como no caso em que calculamos não há cisalhamento, esse já seria o plano principal de tensões, assim:
Sabendo que o plano de tensões principal e o plano de cisalhamento máximo ocorrem a uma diferença de rotação de , nossos elementos ficam:
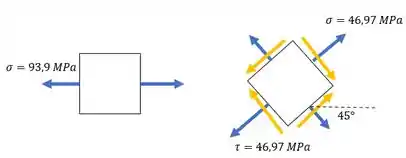
Repara que a orientação é no sentido horário. A gente percebe isso ao montar o círculo de Mohr. Para chegar no estado de cisalhamento máximo, precisamos girar nesse sentido.