Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 38
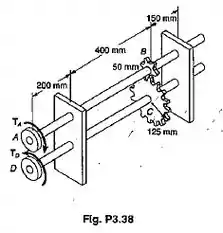
As especificações de projeto para o sistema eixo-engrenagem mostrado requerem que os mesmo diâmetros sejam usados para ambos os eixos e que o ângulo de torção da polia A, quando ela está sujeitoa a um torque de 226 kN.m, não deve exceder a , mantida fixa a polia D. Determinar o diâmetro necessário dos eixos, se ambos são de aço e
Passo 1
Inicialmente temos para a engrenagem B
Para engrenagem
Onde
Passo 2
Calculando então os torques
Já as deformações será expressas por
Como a polia D é mantida fica
Trazendo o valor de que encontramos logo acima
Para teremos
Passo 3
O diâmetro baseado no toruqe é
Onde o maior toruqe será
Onde e dp enunciado.
Isolando então o c teremos
Passo 4
Calculando o diâmetro baseado no limite de rotação
Onde .
Logo
Entã o diâmetro escolhido será o maior, no caso,