Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 39

Resolva o problema 3.38, considerando que ambos são feitos de um latão com G = 39   G P a   e   τ a d m = 55   M P a

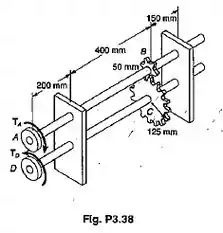
Passo 1

Inicialmente temos para a engrenagem B

∑ M B = 0

r B F - T A = 0 → F = T B / r B

Para engrenagem

Σ M C = 0

r c F - T D = 0

T D = r a F = r c r B T A = n T B

Onde

n = r c r B = 125 50 = 2,5

Passo 2

Calculando então os torques

T A B = T A = T B

T C D = T C = n T B = n T A

Já as deformações será expressas por

ϕ C / D = T C D L G J = n T A L G J

ϕ A / B = T A B L G J = T A L G J

Como a polia D é mantida fica

ϕ D = 0

ϕ C = ϕ D + ϕ C D = 0 + n T A L G J

r B ϕ B = - r c ϕ c

ϕ B = - r c r B ϕ c = - n ϕ c

Trazendo o valor de ϕ c que encontramos logo acima

ϕ B = - n n T A L G J = - n 2 T A L G J

Para ϕ A teremos

ϕ A = ϕ c + ϕ B C = n 2 T A L G J + T A L G J = ( n 2 + 1 ) T A L G J

Passo 3

O diâmetro baseado no toruqe é

τ m = T m c J = 2 n T A π c 3

Onde o maior toruqe será

T m = T C D = n T A

Onde T A = 226   N . m e τ = 83   M P a   dp enunciado.

Isolando então o c teremos

c = 2 n T A π τ m 3 = 2 × 2,5 × 2 , 26 × 10 2 π × 55 000 × 10 3 3 = 0,0 178   m

d = 2 c = 0,0 356   m

Passo 4

Calculando o diâmetro baseado no limite de rotação

ϕ = 7,5 ° = 0,1309   r a d

ϕ = n 2 + 1 T A L G J = 2 × 7,25 × T A L π c 4 G

Onde L = 0,2 + 04 = 0,6 .

c =   2 × 7,25 × T A L π ϕ G 4 = 2 × 7,25 × 2 × 10 2 × 0,6 π × 39 000 × 10 6 × 0,1309 4 = 0,01 815   m

Logo

d = 2 c = 0,03 63   m

Entã o diâmetro escolhido será o maior, no caso, d = 0,03 63   m m

Resposta

d = 0,03 6 3   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As extremidades A e D de dois eixos maciços de aço, AB e CD, estão engastadas enquanto as extremidades B e C são conectadas por engrenagens, como indicado. Sabendo-se que a tensão de cisalhamento admi
Um eixo maciço e um eixo vazado são feitos de mesmo material e têm o mesmo peso e o mesmo comprimento. Expressando por n a reção c 1 / c 2 , mostrar que a relação T m / T v , entre o torque T m do eix
Desenvolver uma expressão aproximada para o ângulo de torção de um eixo, de forma de tronco de cone no Prob 3.56, substituindo o tronco de cone por n eixos cilíndricos de iguais comprimentos e raios r
Desenvolver uma expressão aproximada para o ângulo de torção de um eixo, de forma de tronco de cone no Prob 3.56, substituindo o tronco de cone por n eixos cilíndricos de iguais comprimentos e raios r
Uma placa anelar de latão G = 39G P a de espessura t = 6,36m m é usada para conectar o eixo de latão A B , de comprimento L 1 = 50m m e raio r 1 = 30m m , ao tubo de latão C D de comprimento L 2 = 250