Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 41

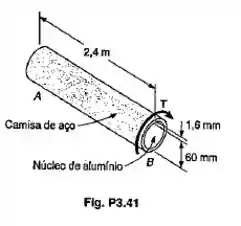
Um eixo composto mostrado consiste em uma camisa de aço ( G a = 77 G P a ) com 1,6 mm de espessura, colado a um núcleo aluminio ( G a l = 26   G P a ) com diâmetro de 60 mm. Sabendo-se que o eixo é submetido a um torque T de 900 N.m é aplicado em B, determinar: (a) a máxima tensão de cisalhamento na camisa do latão; (b) a máxima tensão de cisalhamento no núcleo de aço; (c) o ângulo de torção de B.

Passo 1

Para começar, teremos

G a l = 26   G P a

G a = 77   G P a

T = 900   N . m = T a + T a l

Calculando então cada momento de inércia temos

J a = π 2 31,6 × 10 - 3 4 - 30 × 10 - 3 4 = 2,94 × 10 - 7   m 4

J a l = π 2 30 × 10 - 3 4 = 1,27 × 10 - 6

Passo 2

Sabrmos ainda que o ϕ a = ϕ a l ,   logo

T a 2 2,94 × 10 - 7 × 77 × 10 9 = T a l 2 1,27 × 10 - 6 × 26 × 10 9

Com isso temos a relação

T a = 0,69   T a l

Temos então do enunciado

T = 900   N . m = T a + T a l

900 = T a l + 0,69   T a l

T a l = 533,94     N . m

Voltando com a relação

T a = 0,69   T a l

T a = 368,42   N . m

Passo 3

Com isso podemos começar a calcular as máximas tensões admissíveis

(a) para o alumínio

τ a l = T a l c a l J a l = 533,94 × 30 × 10 - 3 1,27 × 10 - 6 = 16 , 61   M P a

Passo 4

Para (b) o aço

τ a = T a c a J a = 368,42 × 3 1,6 × 10 - 3 2,94 × 10 - 7 = 39,6     M P a

Passo 5

Na letra (c) somos pedido o ângulo. Faremo então

ϕ a = ϕ a l = T a l L a l J a l G a l = 533,94 × 2 , 4 4,128 × 10 - 7 × 26 × 10 9 = 0 , 119   r a d = 6,84 °

Resposta

a )   τ a l = 16 , 61   M P a

b ) τ a = 39,6   M P a

c )   ϕ = 6,84 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra cilíndrica maciça AB e o tubo CD são ambos unidos por um pequeno cilindro E. A barra cilíndrica AB é de aço, com G a = 77G P a e τ a d m a = 84M P a ; enquanto que o tubo CD é de latão, com G
Sabendo-se que um torque T de 2,3k N m é aplicado ao cilindro E do Prob. 3.49, determinar (a) a máxima tensão de cisalhamento na barra cilíndrica AB; (b) a máxima tensão de cisalhamento no tubo CD
Uma placa anelar de espessura t e módulo de elasticidade transversal G é usada para conectar o Eixo AB de raio r 1 ao tubo CD de raio interno r 2 . Sabendo-se que o torque T é aplicado à extremidade A
Uma placa anelar de espessura t e módulo de elasticidade transversal G é usada para conectar o Eixo AB de raio r 1 ao tubo CD de raio interno r 2 . Sabendo-se que o torque T é aplicado à extremidade A
As extremidades A e D de dois eixos maciços de aço, AB e CD, estão engastadas enquanto as extremidades B e C são conectadas por engrenagens, como indicado. Sabendo-se que um torque T de 4 kNm é aplica