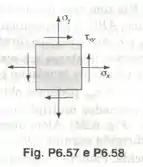
Para um estado plano de tensões é conhecido que as tensões, normal e de cisalhamento, são dirigidas como indicado e que σ x = 90M P a , σ y = 45M P a e σ m í n = 30M P a í . Determinar: (a) a orientação dos planos principais; (b) a tensão principal σ m á x á ; (c) a máxima tensão de cisalhamento, no plano.

(a) θ p = 26,57 ° no sentido anti-horário e θ p 2 = 63,43 ° no sentido horário.(b)σ m á x = 105M P a á (c)τ m á x = 37,5M P a á

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 57

Para um estado plano de tensões é conhecido que as tensões, normal e de cisalhamento, são dirigidas como indicado e que , e . Determinar: (a) a orientação dos planos principais; (b) a tensão principal ; (c) a máxima tensão de cisalhamento, no plano.

Passo 1

a) O que a gente precisa fazer aqui é usar o Círculo de Mohr para descobrir o ângulo e seu sentido, porque ele define a orientação dos planos principais.

E como a gente faz isso? Vamos tentar montar esse círculo com as informações que a gente tem. Vamos listar:

- a tensão normal no eixo é positiva porque está saindo da seção e vale:

- tensão normal mínima vale:

- vamos considerar o cisalhamento positivo, como está na figura.

Bora começar!

Passo 2

Achando a coisinhas que a gente precisa para montar o Círculo de Mohr: vamos calcular as coordenadas de , , o centro e o raio . Temos que:

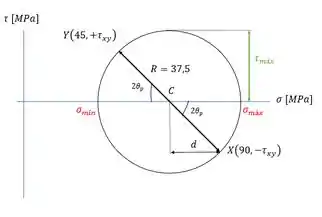
Colocando essas coisas no Círculo:

Passo 3

Olhando para esse círculo lindão, vemos que podemos dizer que:

E a gente precisa girar nossa reta no sentido anti-horário para chegar no eixo horizontal. Para descobrir o ângulo do outro plano é só substrair dele. Dá:

Só que no sentido horário.

Passo 4

b) Agora a gente quer a tensão principal . Podemos achar ela pela expressão:

Passo 5

c) Agora a gente quer a tensão de cisalhamento máximo. Aqui é só lembrar que:

Resposta

(a) no sentido anti-horário e no sentido horário.

(b)

(c)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método da sec 7.4 resolver o problema 7.4

Usando o método da sec 7.4 resolver o problema 7.5

A viga AB suporta duas cargas concentradas P e Q. A tensão normal devido a flexão na borda inferior da seção transversal da viga é de + 55MPa em D e 37,5 MPa em F. Pede-se a) desenhar os diagramas de

As vigas AB, BC e BD tem seções transversais como mostrado e são articuladas por pinos conectores em B e C. Sabendo se que σadm= 150 MPa na tração σadm= -120 MPa na compressão a) o maior valor admissí

A viga AB tem uma seção transversal retangular de largura b constante e altura h variável. Sabendo que a viga deve ser de resistência constante, expressar h em termos de x, L e ho.