Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 78

Para o estado plano de tensões indicado, determine o intervalo de valores de τ x y para o qual a tensão de cisalhamento máxima é igual ou menor que 60   M P a .

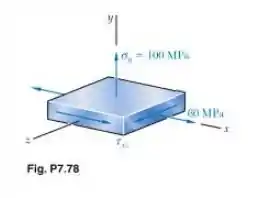
Passo 1

Fala aí, galerinha. Tudo bem com vocês? Bora matar esse livro.

O primeiro passo é listar os dados fornecidos pelo problema. Sabemos que:

σ x = 60   M P a

σ z = 0

σ y = 100   M P a

Calculando a tensão média:

σ m é d = σ x + σ y 2 = 30   M P a

Calculando agora a diferença média das tensões:

u = σ x - σ z 2 = 30   M P a

Passo 2

Portanto, temos que:

σ m á x = σ y = 100   M P a

σ m í n = σ m á x - 2 τ m á x = 100 - 2 × 60 = - 20   M P a

O raio é dado por:

R = σ m é d - σ m í n

R = 30 - ( - 20 ) = 50   M P a

Portanto:

σ a = σ m é d + R = 30 + 50 = 80   M P a < σ y

Passo 3

Como esta tensão é menor que σ y ,   vamos calcular o τ x y através de:

R = u 2 + τ x y 2

Logo, isolando τ x y   e substituindo os outros valores:

τ x y = ± 40   M P a

Ou seja:

- 40   M P a ≤   τ x y ≤ 40   M P a

Resposta

- 40   M P a ≤   τ x y ≤ 40   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Prove que a expressão σ x ' σ y ' - τ x ' y ' 2 , onde σ x ' , σ y ' e τ x ' y ' são componentes da tensão ao longo dos eixos retangulares x ' e y ' , independe da orientação destes eixos. Também
Determinar os planos principais e as tensões principais para o estado plano de tensões, resultante da superposição dos dois estados planos de tensões mostrado.
Determinar os planos principais e as tensões principais para o estado plano de tensões, resultante da superposição dos dois estados planos de tensões mostrado.
Determinar os planos principais e as tensões principais para o estado plano de tensões, resultante da superposição dos dois estados planos de tensões mostrado.
Para o estado plano de tensões mostrado, determinar a máxima tensão de cisalhamento, quando: (a) σ z = 0M P a ; (b) σ z = + 60M P a ; (c) σ z = - 60M P a .