(a) Prove que a expressão , onde , e são componentes da tensão ao longo dos eixos retangulares e , independe da orientação destes eixos. Também mostre que a referida expressão representa o quadrado da tangente, traçada a partir do sistema de coordenadas do círculo de Mohr. (b) Usando a propriedade invariante estabelecida na parte (a), expressar a tensão de cisalhamento em termos de , e das tensões principais e .
Passo 1
a) Ele quer que a gente ache a expressão de:
E mostre que ela independe da orienteção dos eixos, ou seja, de .
Vamos montar um círculo de Mohr genérico para esses eixos e , para perceber umas coisinhas:
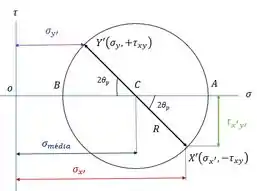
Dessa figura, a gente tira umas relações geométricas:
Passo 2
Vamos escrever a expressão que ele pediu, usando essas relações aí:
Aí a gente lembra daquela identidade trigonométrica bacana:
Olha só! Reduzimos nossa expressão e provamos que ela não depende de .
Passo 3
Agora a gente quer mostrar que isso é o quadrado da tangente saindo de . O que isso significa? Que isso é numericamente igual ao quadrado do comprimento do segmento entre e um ponto tangente ao nosso círculo.
Olha essa figura bonita. O ponto de tangência é .
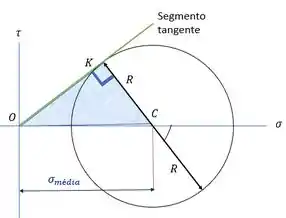
Queremos então provar que o nosso resultado é igual ao quadrado do segmento . Percebe que ele é um cateto de um triângulo retângulo. Então a gente pode usar Pitágoras para escrever:
Já que:
E no passo anterior a gente viu que isso é igual a nossa expressão:
Uhul!
Passo 4
b) Essa propriedade diz que o valor de:
É o mesmo para qualquer ângulo . Vamos usar isso para expressar , usando , , e .
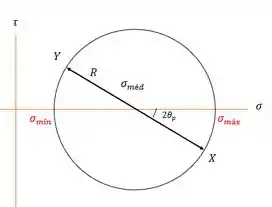
Na orientação , essa expressão fica:
E para a orientação dos eixos principais:
Mas a propriedade diz que esses valores são iguais, então:
É isso! (a gente só não consegue definir o sinal mesmo dessa raiz, mas é isso aí)
Resposta
(a) prova nos passos
(b)