Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas Revisão - Ex. 160
O estado plano de tensões mostrado ocorre em uma barra feita de uma classe de aço, cuja tensão de escoamento à tração é de . Determinar o coeficiente de segurança, em relação ao escoamento, usando:
- O critério da máxima tensão de cisalhamento;
- O critério da máxima energia de distorção.
Passo 1
Fala galera, vamos fazer esse exercício de maneira muito simplificada para ficarmos muito tranquilos. Para o fator de segurança, precisamos seguir duas linhas de raciocínio.
Primeiro temos que definir as tensões principais, sabemos que a fórmula é dada por:
Sabemos que:
E ainda temos que pensar que temos uma tensão fora do plano que não observamos dada por:
Sendo assim, quando formos determinar a máxima tensão cisalhante, devemos usar o seguinte cálculo:
E assim determinamos as nossas máximas tensões, porém para o fator de segurança precisamos tanto da máxima tensão, quando da tensão resistente, para a tensão resistente temos os seguintes critérios a serem usados:
- Critério da máxima tensão de cisalhamento (ou critério de Tresca)
- O critério da máxima energia de distorção (ou critério de von mises)
Se considerarmos o critério de tresca, a máxima tensão cisalhante resistente que age na nossa estrutura é dada por:
Assim o fator de segurança é dado por:
Esse critério é um pouco diferente, porque ele, a partir das tensões principais, determina uma nova tensão principal total. Essa tensão principal total será a que vamos usar no fator de segurança, sendo assim temos que:
E o fator de segurança é dado por:
Agora que já sabemos o que fazer, podemos ficar mais tranquilos, vamos nessa?
Passo 2
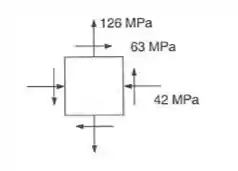
Sabemos que o nosso elemento é dado por:
E agora podemos definir a nossas tensões principais, com isso temos que:
Considerando ainda uma tensão fora do plano, tem-se que:
Com isso temos que:
Agora podemos ira para os fatores de segurança.
Passo 3
Pelo critério da máxima tensão de cisalhamento temos que:
Sabemos que:
Assim o fator de segurança é dado por:
Passo 4
Pelo critério da máxima energia de distorção temos que:
E determinamos que:
E o fator de segurança dado por:
E assim resolvemos o nosso problema, viu como era bem tranquilo? Bora partir para a próxima então.