Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas Revisão - Ex. 158
um extensômetro é colado horizontalmente, numa superfície cilíndrica de um vaso de pressão de de diâmetro externo e de espessura da parede. Sabendo-se que e e que o extensômetro indica , determinar:
- As três deformações especificas principais na superfície cilíndrica do vaso;
- As tensões principais na parede;
- A pressão medida dentro do vaso.
Passo 1
Fala ai galera, agora vamos para uma questão que vamos usar dois conceitos muito legais que aprendemos. Um desses conceitos é o cálculo das tensões principais que sabemos que devemos usar as fórmulas abaixo para o caso de estruturas cilíndricas.
- Sabemos que a nossa tubulação é cilíndrica e não esférica, nesse caso, usaríamos as seguintes equações:
- Sabemos que o nosso diâmetro dado, é o diâmetro externo, ou seja, precisamos descontar a espessura, sendo assim temos que:
- E sabemos que é a espessura
- é a pressão que age na nossa estrutura
Até aqui tudo certo, certo? Mas pensa o seguinte, ele nos da um dado de deformação, como a deformação se relaciona com a tensão? Muito simples, basta lembrar que a formula da deformação especifica em função da tensão é de:
Como estamos pensando em um vaso de pressão, sabemos que as tensões que irão aparecer são dadas por:
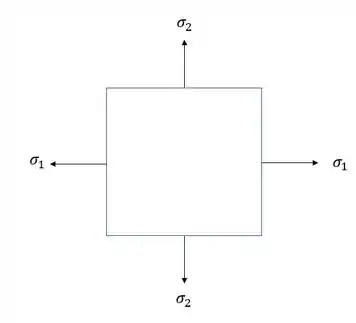
Como não temos tensões cisalhantes, essas já são as tensões principais. Se dividirmos tudo pelo modulo de elasticidade, teremos que:
Porém, queremos as deformações em cada um dos planos, e por isso temos que lembrar da contribuição que uma tensão em um sentido, produz no outro, sendo assim, as deformações que de fato ocorrem no nosso elemento são dadas por:
E assim teremos as deformações principais do nosso elemento, lembrando que nos vasos de pressão consideramos que . Agora que já sabemos isso vamos ao nosso problema.
Passo 2
Sabemos pelo enunciado que:
Calculando o raio, temos que:
Calculando a tensão, teremos que:
E assim resolvemos metade do nosso problema.
Passo 3
Vamos agora para as análises das nossas deformações:
A deformação na direção 2 é dada por:
A deformação na direção 3 é dada por:
Perceba que o nosso extensômetro está exatamente na direção dois do nosso elemento, ou seja, no nosso enunciado é dito que foi marcado no extensômetro o seguinte:
Substituindo temos que:
E assim resolvemos o nosso item c). pode parecer estranho resolvermos ele primeiro, mas é exatamente a solução dele que vai permitir que resolvamos os outros. Por exemplo, agora com esse dado, podemos obter as deformações.
E assim também temos as deformações principais, que é o nosso item a).
Passo 4
E o item b) é simples, como temos as tensões e podemos determinar as máximas tensões do nosso elemento, sendo assim, temos que:
E assim resolvemos tudo, show? Bora para o próximo passo.