Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas Revisão - Ex. 153
Para o estado plano de tensões mostrados, determinar:
- Os planos principais
- As tensões principais
- A máxima tensão de cisalhamento.
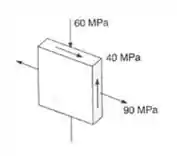
Passo 1
Então galerinha, vamos pegar os macetes desse exercício para ficar mais fácil resolver qualquer exercício que encontrarmos sobre isso.
Nessa questão temos dois objetivos, que são determinar os planos de tensões principais, que podemos descobrir pela seguinte equação:
E sabemos que:
E a segunda opção é definir as tensões principais, sabemos que a fórmula é dada por:
Sabemos que:
E assim determinamos as nossas máximas tensões e os planos em que elas ocorrem, vamos lá então:
Passo 2
Sabemos que o nosso elemento é dado por:
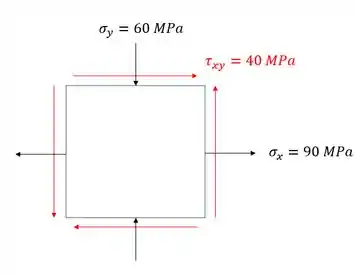
Então vamos definir primeiro os planos principais:
E agora podemos definir a nossas tensões principais, com isso temos que:
E por fim, a tensão cisalhante máxima vai ser exatamente o nosso R calculado, sendo assim teremos que:
Bora pra próxima questão porque essa já ta feita, vamos nessa?