Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 112b
Resolver o , assumindo que a força é horizontal
- Ponto L;
Passo 1
Fala galera, essa questão aqui é uma boa questão para treinarmos tudo que aprendemos até agora, ela vai exigir de nós todos os conhecimentos que tivemos até agora para cálculo de tensões, então, antes de sairmos calculando tensões, vamos entender o que estamos calculando, porque se soubermos os tipos de esforços que agem no ponto pedido, vamos saber quais fórmulas teremos que usar, com isso, vamos esquecer a pressão e vamos imaginar isso como sendo uma barra circular com o esforço da carga P agindo nela, e vamos levar até a região com o ponto L esses esforços, com isso, vamos lá.
- Primeiro – Vista das cargas
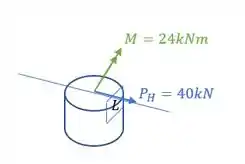
Olhando o nosso problema, podemos ver que o nosso esforço P não possui um ângulo com a horizontal, ou seja, temos que , olhando o tanque de lado, teremos uma visão melhor do nosso ponto L e das forças atuantes, com isso, teremos que:
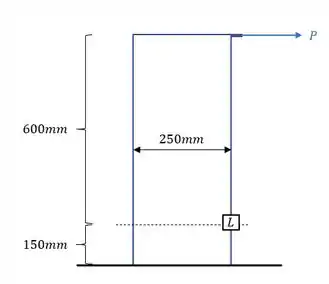
Vamos primeiro levar as cargas para o centro da seção, sendo assim teremos que:
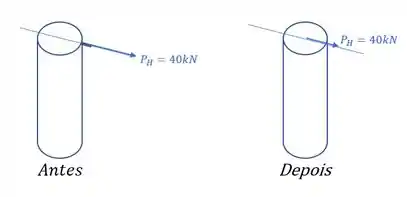
E quando levamos esses esforços para o nível do ponto L, levaremos todos os esforços normalmente, mas vale lembrar que a carga horizontal vai gerar um momento fletor, sendo assim, teremos que:
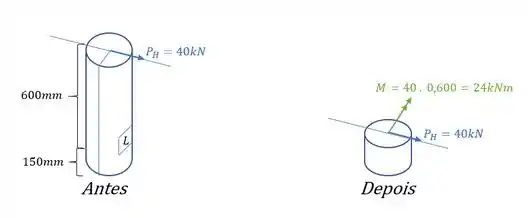
Assim o elemento será definido como:
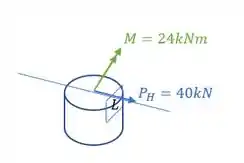
Definido isso, vamos agora entender como as tensões vão funcionar no nosso elemento:
Passo 2
Você lembra como era o nosso elemento infinitesimal quando o mesmo estava sujeito a um conjunto de tensões?
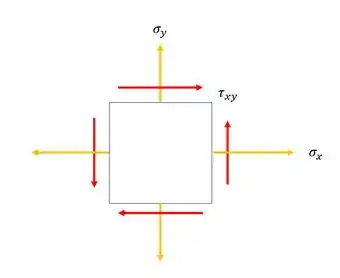
Porém, sempre que tratamos vasos de pressão, ou esferas de pressão, calculávamos um estado de tensões sem tensão de cisalhamento, ou seja, só tensões principais, que é exatamente isso aqui que calculamos:
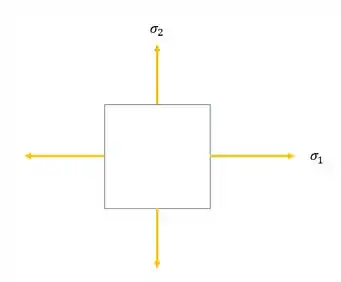
Agora pensa no seguinte, olhando o nosso elemento aqui em baixo, podemos ver o seguinte:
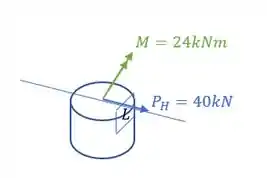
Nesse caso não temos um esforço normal agindo na nossa seção, porém, caso seja pedido o cálculo da tensão normal, podemos usar a seguinte equação.
Em que a A é dada por:
E essa tensão normal, sendo uma compressão, vai diminuir a nossa tensão 2, sendo assim, teremos que:
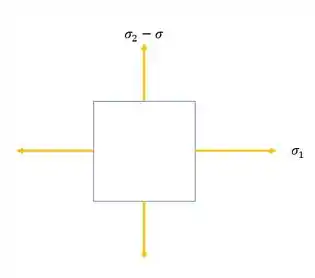
Porém além do normal também temos um momento fletor agindo na nossa seção:
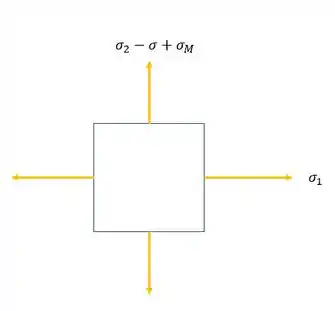
O momento fletor produzirá uma tensão de compressão, ou seja, podemos usar a nossa fórmula sem sinal e subtrair o valor da direção da , ou podemos usar a fórmula normal, mas quando calcularmos ela, sabendo que é compressão, ela deverá ser negativa e no fim, também irá subtrair da nossa tensão 2 e a fórmula que devemos usar, será dada por:
E o nosso elemento ficaria sendo:
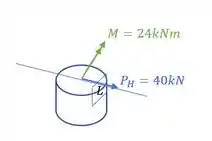
E agora só temos mais uma força a ser avaliada que é a força horizontal, que geraria um cortante na nossa seção, somente se a mesma estivesse no local em que está o ponto K, no local que ela de fato está, o cortante será nulo, porém, caso devêssemos também determinar algo no ponto K, a fórmula a ser usada é.
E assim o nosso elemento será dado por:
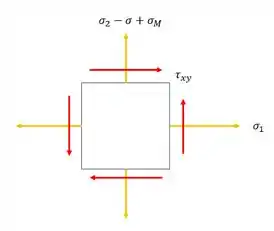
E agora só falta definir essas duas tensões onde as tensões normais são calculadas da seguinte maneira.
- Sabemos que a nossa tubulação é cilíndrica e não esférica, nesse caso, usaríamos as seguintes equações:
- Sabemos que o nosso diâmetro dado, é o diâmetro externo, ou seja, precisamos descontar a espessura, sendo assim temos que:
- E sabemos que é a espessura
- é a pressão que age na nossa estrutura
Até aqui tudo certo, certo? Mas ai entra uma coisa bem legal, lembra que o enunciado quer saber as TENSÕES máximas cisalhante e normal, e agora que temos um elemento infinitesimal, como vamos fazer para determinar as tensões máximas? Só lembrar das nossas fórmulas dadas por:
Sabemos que:
Agora sim temos toda a matéria prima para resolver o nosso problema, vamos nessa??
Passo 3
Com tudo em mãos, vamos definir todas as tensões que agem no nosso elemento, e depois que tivermos o elemento em mãos, ai sim definimos as máximas tensões:
Sabemos pelo enunciado que:
Calculando o raio, temos que:
Calculando a tensão, teremos que:
Como não temos nenhuma força vertical, podemos considerar essa tensão 0:
Pelos dados do enunciado e o que já calculamos, teremos que:
O momento de inércia são duas seções circulares, uma com o raio externo como positivo, e um com raio interno negativo, isso tem o objetivo de acharmos o momento de inércia da parede do tubo, então basta fazer o momento de inércia da seção total menos a inercia da seção interna, assim teremos que:
Pela fórmula teremos que:
Para a posição L já sabemos que a tensão cisalhante se anulará.
Agora precisamos dos elementos infinitesimais, com isso, teremos que:
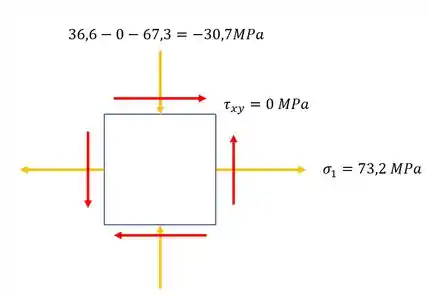
Passo 4
E agora que temos o elemento infinitesimal, precisamos apenas das tensões principais, e essas tensões principais são dadas pela seguinte equação.
E assim já temos a tensão máxima cisalhante agindo no nosso elemento infinitesimal.
As tensões principais normais são dadas por: