Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 29
Para o estado de tensão mostrado, determine o maior valor de para o qual a tensão de cisalhamento máxima no plano da tensão paralela à solda é zero e as tensões principais correspondentes.
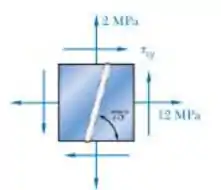
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora estudar mecânica e garantir aquele notão na prova.
Primeiro, vamos determinar o maior valor de para o qual a tensão de cisalhamento máxima no plano da tensão paralela à solda é zero através orientação dos planos pricipais:
Onde , logo:
Passo 2
Em seguida, vamos determinar a tensão máxima. Para isso, temos que:
Agora, para encontrarmos as tensões principais, temos que a tensão é dada por:
Logo:
Substituindo:
É isso, galera.
Resposta
Exercícios de Livros Relacionados
Mostre que a soma das três medidas de deformação feitas com uma roseta de 60° é independente da orientação da roseta e igual a ϵ 1 + ϵ 2 + ϵ 3 = 3 ϵ m e d Em que ϵ m e d é a abscissa do centro do círc
Um único extensômetro é colado em um eixo de aço com seção transversal cheia de 101,6 mm de diâmetro formando um ângulo β = 25 ° com uma linha paralela ao centro do eixo. Sabendo que G = 79,3 GPa, det
Resolva o Problema 7.150 considerando que a roseta no ponto A indica as seguintes deformações: ϵ 1 = - 3 0μ ;ϵ 2 = + 25 0μ ;ϵ 3 = + 1 0 0μ
Uma força axial centrada P e uma força horizontal Q são aplicadas ao ponto C da barra de seção retangular mostrada na figura. Uma roseta de deformação de 45° na superfície da barra no ponto A indica a
As deformações específicas determinadas por uma roseta fixada, à superfície de um elemento de máquina são, conforme mostra a figura ϵ 1 = - 93,1μ ;ϵ 2 = + 385μ ;ϵ 3 = + 210μ Determine (a) a orientação