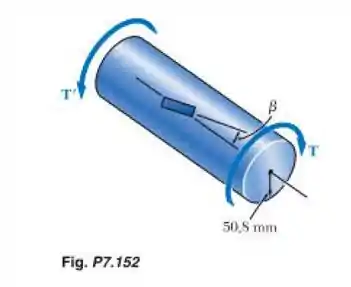
Um único extensômetro é colado em um eixo de aço com seção transversal cheia de 101,6 mm de diâmetro formando um ângulo com uma linha paralela ao centro do eixo. Sabendo que G = 79,3 GPa, determine o torque T indicado por uma leitura no extensômetro de 300.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos precisar utilizar a equação para a tensão de cisalhamento gerada por torção, dada por:
Em que T é o torque aplicado, c é a distância do centro do eixo até o ponto de interesse e J é o momento polar de inércia. Então, c e J serão propriedades geométricas, no entanto vamos precisar escrever o valor do torque em função da deformação e do módulo de cisalhamento dado no enunciado. Para isso vamos precisar encontrar a deformação no ponto com inclinação , que é a posição do extensômetro para a qual temos a leitura de 300. Para isso vamos precisar do auxílio do círculo de Mohr, então vamos começar encontrando as deformações. Então bora lá!
Passo 2
Tá legal! Sabemos que nesse caso não temos tensão normal no sistema, então teremos:
Então, as deformações nas direções x e y serão:
E, a nossa deformação de cisalhamento será:
Só lembrando que para o eixo do círculo de Mohr, nós desenhamos , então a equação acima pode ser escrita como:
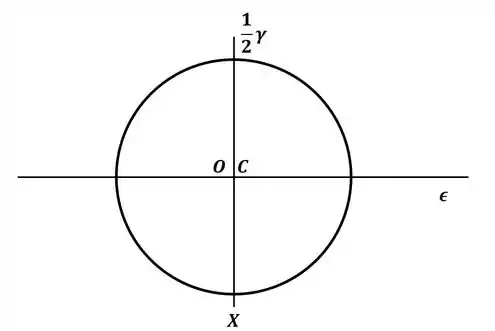
Beleza! Com esses pontos podemos desenhar nosso círculo de Mohr, que será dado por:
Passo 3
Agora, através do círculo de Mohr do passo 2, é fácil verificar que o raio do círculo será a própria deformação de cisalhamento dividida por 2, ou seja:
Agora, nós vamos rotacionar o ponto X de um ângulo no elemento diferencial, ou seja, rotacionar o círculo de Mohr de , então teremos:
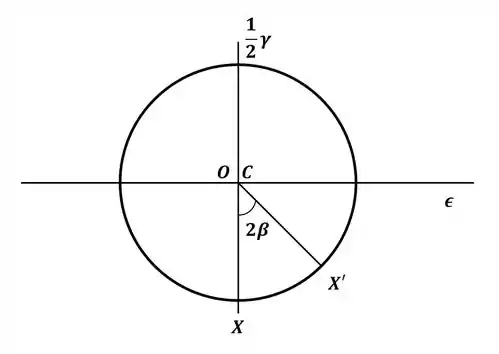
Então, para esse ponto, teremos a deformação em x igual a:
E, isolando a tensão de cisalhamento dessa equação, teremos:
Passo 4
Agora vamos utilizar a equação para a tensão de cisalhamento que escrevemos lá no passo 1, dada por:
No nosso caso, a distância c será o próprio raio do eixo, pois o estamos lidando com o elemento diferencial na superfície do eixo, então teremos:
Agora, para uma seção circular maciça, o momento polar de inércia é dado por:
Em que c é o raio do eixo. Então, substituindo os valores conhecidos nessa equação, teremos:
Agora podemos substituir a expressão que encontramos para a tensão de cisalhamento no passo 3 na equação do passo 4, chegando em:
Isolando o torque dessa equação e substituindo os valores conhecidos, chegamos em:
Feshooow!