Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 149
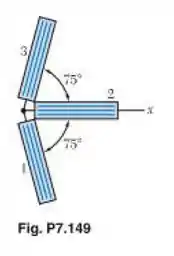
As deformações específicas determinadas por uma roseta fixada, à superfície de um elemento de máquina são, conforme mostra a figura
Determine (a) a orientação e a intensidade das deformações específicas principais no plano da roseta e (b) a máxima deformação por cisalhamento no plano.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar a equação 7.44 vista nesse capítulo, que nos dá a deformação ao longo de um eixo qualquer, dada por:
E vamos utilizar essa relação nas 3 direções, lembrando que aqui estamos lidando com deslocamentos no círculo de Mohr, então para cada 1° de rotação na roseta, temos 2° no círculo. Fazendo isso, chegaremos em expressões para as direções 1, 2 e 3, depois disso é só resolver o sistema para chegar nos valores para as deformações. Com esses valores, conseguimos utilizar a equação 7.52, dada por:
Para encontrar a orientação das deformações específicas principais pedidas na letra (a). Depois disso, vamos precisar encontrar as deformações principais, que são dadas por:
Então precisamos calcular a deformação média e o raio do círculo de Mohr. Feito isso, faltou só calcular a tensão de cisalhamento máxima no plano, e nesse caso, sabemos que ela será o diâmetro do círculo de Mohr. Então bora lá!
Passo 2
Beleza! Vamos escrever a deformação na direção 1, que está a um ângulo da referência, utilizando a equação vista no passo 1. Então teremos:
Beleza! Vamos guardar essa expressão aqui por enquanto. Agora vamos escrever a deformação na direção 2, que está a uma rotação de da referência, então teremos:
Beleza! Já conseguimos o valor de . Agora, vamos escrever a expressão para a deformação na direção 3, que está a uma rotação de da referência, então teremos:
Agora, nós vamos somar as equações para e , chegando em:
Simplificando essa expressão, chegamos em:
Isolando dessa equação, teremos:
Substituindo os valores conhecidos, chegamos em:
Passo 3
Agora vamos pegar a equação 1 e subtrair da 3, obtendo:
Isolando a deformação de cisalhamento e substituindo os valores conhecidos, teremos:
Agora, podemos finalmente encontrar a direção principal através de:
E, como sabemos que a outra direção principal fica a 90° de inclinação no elemento diferencial (ou seja, a 180° no círculo de Mohr), então a outra direção será:
Passo 4
Ainda na letra (a), precisamos encontrar as deformações principais, que são dadas por:
Então, vamos começar calculando a deformação média, que é dada por:
Agora, para o raio do círculo de Mohr, teremos:
Então, as deformações principais serão:
Beleza! Agora sim terminamos a letra (a). Bora pra (b) que ela é rapidinha!
Passo 5
Agora, para a letra (b), como sabemos que a deformação por cisalhamento máxima no plano será o diâmetro do círculo de Mohr, nós temos:
Substituindo o valor do raio encontrado no passo 4, chegamos em:
Shooow! Acabamos mais um!! Valeeu!