Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 150
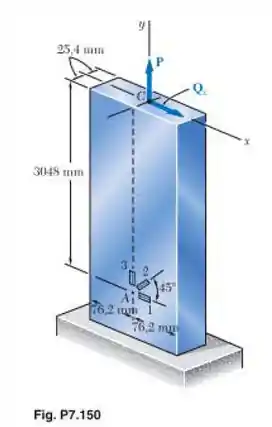
Uma força axial centrada P e uma força horizontal Q são aplicadas ao ponto C da barra de seção retangular mostrada na figura. Uma roseta de deformação de 45° na superfície da barra no ponto A indica as seguintes deformações:
Sabendo que E = 200 GPa e , determine as intensidades de P e .
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos precisar descobrir as tensões normais nas direções x e y, que serão dadas por:
A partir da tensão normal em y, poderemos encontrar a força P aplicada. Então, para achar a força vamos partir para a análise do cisalhamento, onde teremos a tensão de cisalhamento dada por:
Em que V é a força de cisalhamento (nossa força ), Q é o momento de área da seção, I o momento de inércia e t a espessura da seção naquele ponto. Então, para isso vamos precisar calcular todos esses termos, depois é só isolar V e descobrir nosso valor de . Então bora lá!
Passo 2
Tá legal! Vamos começar escrevendo as deformações nas direções x e y através da roseta dada na figura e das deformações fornecidas, então teremos:
E a nossa deformação de cisalhamento será dada por:
Agora podemos calcular o valor da tensão normal na direção x, que conforme vimos no passo 1, será dada por:
Substituindo os valores conhecidos, temos:
Agora, vamos calcular a tensão normal na direção y, através de:
Substituindo os valores conhecidos, chegamos em:
Então, sabendo que a tensão é dada pela força sobre área, na direção y teremos:
Isolando P dessa equação e substituindo os valores conhecidos, temos:
Boa, encontramos o valor de P. Agora vamos começar a caçada pelo valor de .
Passo 3
Então, para encontrar nossa força , iremos utilizar a equação vista no passo 1, dada por:
Sendo que . Então vamos começar calculando o momento de inércia da seção, que será dado por:
Agora, o momento de área, que será dado pela metade da seção transversal, já que a força está aplicada no centro da seção, então teremos:
Agora, a espessura da seção será a própria largura dela, ou seja:
Agora falta só descobrir o valor da tensão de cisalhamento, para isso, sabemos que ela pode ser escrita como:
Já temos a deformação de cisalhamento vista lá no passo 2. Precisamos agora do módulo de cisalhamento, que por sua vez é dado por:
Então, nossa tensão de cisalhamento será:
Então, isolando a força cortante V, que é a nossa , da equação para a tensão de cisalhamento, teremos:
E, substituindo os valores conhecidos, chegamos em:
Shoow! Terminamos mais um, valeeu!