Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 115
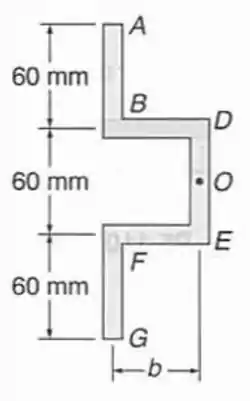
Uma viga de parede fina com espessura uniforme tem a seção transversal mostrada. Determinar a dimensão , para que o centro de cisalhamento da viga esteja localizado no ponto indicado.
Passo 1
Para acharmos a localização do ponto , ou seja, a distância vamos fazer o seguinte passo a passo:
- Achar a tensão cisalhante.
- Calcular, por meio de integral, a força interna atuante na bara.
- Com essa força achar o momento atuante.
Passo 2
Neste problema teremos que dividir a seção em duas partes, parte e a parte porque cada uma delas vai gerar um momento em relação a . Para achar a tensão cisalhanete temos que encontrar o momento estático de cada parte, fazendo para .
É importante lembrar que vamos pegar apenas um pedaço da barra que vai até certo ponto e não a barra inteira, de forma que possamos integrar isso depois.
Agora podemos achar a tensão cisalhante:
Passo 3
Por meio de uma integral vamos achar a força atutante na barra :
Transformando
Passo 4
Agora vamos executar os mesmos dois passos para a parte :
É importante lembrar que vamos pegar apenas um pedaço da barra que vai até certo ponto e não a barra inteira, de forma que possamos integrar isso depois.
Agora podemos achar a tensão cisalhante:
Passo 5
Por meio de uma integral vamos achar a força atutante na barra :
Transformando
Passo 6
Agora a gente vai pegar as duas forças e calcular o momento, mas é importante lembrar que a gente calculou só metade da barra então vamos ter o seguinte no final das contas:
Onde é o momento da força de , ambas tem o mesmo sentido. Enquanto é o momento da força sentidos opostos, logo formam um binário:
Substituindo:
Igualando: