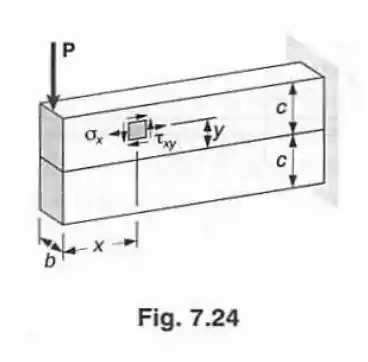
Usando a equação derivada da parte do Prob. 7.126, mostrar que, em qualquer seção transversal da viga da Fig. 7.24, onde , o maior valor de ocorre para . (Sugestão: Denotando por , o valor correspondente de para e as posições e , escrever uma equação definindo os valores de para , e mostrar que, para , a única raiz real dessa equação é ).

Com essa substituição vamos ficar com o seguinte:

Beleza! Agora o problema também sugere estabelecer um para quando , ou seja, . Vamos fazer isso!

Galera, ainda seguindo os passos da sugestão da questão vamos considerar que olha só!

Desenvolvendo vamos obter:

Agora fica mais fácil para elevar ambos os lados da equação ao quadrado:

Colocando em evidência:

Agora vamos tentar acabar com as frações!

Utilizando o produto notável

Pessoal, como a gente já sabe que vai ser uma raiz a gente não pode cortar o termo ok?

Agora temos uma relação beeem mais simples entre e , correto?

Lembrando que a gente tem que mostrar que, para , a única raiz real dessa equação é .

De fato, para que essa equação esteja correta, considerando que é se !

Podemos mostrar isso considerando que , assim vamos poder fazer a simplificação:

Vamos substituir

Essa equação de terceiro grau irá ter duas raízes complexas e uma negativa, como é uma dimensão real sobre outra, então é claro que nenhuma dessas três raízes pode ser solução. Desta forma, realmente é a única solução =D