Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 125
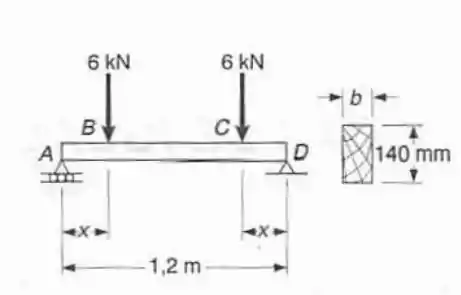
Para a viga com o carregamento mostrado, determinar a largura da viga e a distância , para que a tensão normal máxima e a tensão máxima de cisalhamento na viga sejam simultaneamento iguais a:
Passo 1
Oi, fala aí, galerinha!!! Para resolver esse problema a gente vai seguir o seguinte passo a passo:
- Calcular a força cortante, o momento fletor e achar o momento fletor máximo e a força cortante máxima.
- Com o momento fletor máximo e a força cortante máxima vamos poder achar as máximas tensões normal e cisalhante, utilizando também o perfil da seção para calcular o módulo de resistência .
Então partiu pro exercício!
Passo 2
A primeira coisa que vamos fazer é o diagrama de forças, de modo a achar as resultantes:
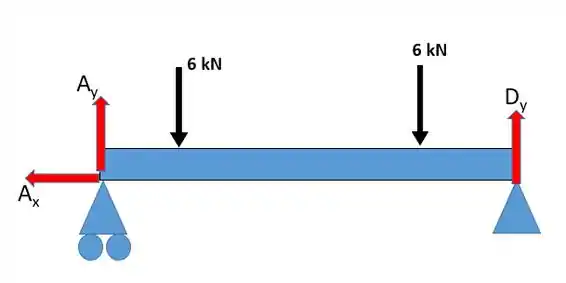
Agora, através das equações da estática vamos achar as reações. É possível perceber que só existe uma força no horizontal logo ela é nula, assim, .
Partindo para as forças em :
Como temos um problema simétrico:
Passo 3
Agora vamos calcular o momento fletor máximo e a força cortante máxima. Este exercício torna isso mais simples visto que temos um problema simétro, logo a força cortante máxima ocorre nos pontos de apoio enquanto o momento fletor máximo ocorre no centro da barra:
Passo 4
Agora vamos calcular a máxima tensão:
Perceba que temos de calcular o módulo resistente :
Calculando o momento de inércia:
Como:
Temos:
Substituindo na tensão:
Como isso tem que ser igual a
Show vamos guardar essa equação e partir para a tensão cisalhante!
Passo 5
A tensão cisalhante para seções retangulares pode ser calculada como:
Como
Passo 6
Agora é só substituir na equação que separamos no passo 4:
Lembrando que a força está em , logo: