Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 51
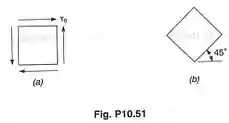
Para o estado de tensões mostrado na Fig. a, determinar as tensões sobre um elemento orientado como mostrado na Fig. b. Calcular a densidade de energia de deformação específica, inicialmente dado pelo estado de tensões da Fig. a, depois usando a Fig. b. Equacionar os dois resultados obtidos, e mostrar que:
Passo 1
Fala, pessoal! Essa é uma questão de energia de deformação que pode te preparar bem pra sua prova! Então vamos nessa, resolver!
O enunciado pede três coisas pra gente. Primeiro, ele quer que a gente determine quanto valem a tensão de cisalhamento e as tensões normais e do elemento da Fig. b, sabendo que o estado de tensões dele é igual ao estado mostrado na Fig. a, onde e .
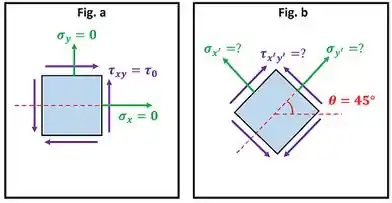
Para achar as tensões da Fig. b, temos que usar as fórmulas de estado plano de tensões abaixo.
Em segundo lugar, o enunciado pede para a gente calcular a densidade de energia de deformação específica do estado de tensões da Fig. a e a densidade de energia de deformação específica do estado de tensões da Fig. b . Elas podem ser calculadas com a equação 10.26 do livro!
Por fim, o enunciado pede que a gente iguale com para mostrar que:
Sabendo de tudo isso, vamos partir para a resolução!
Passo 2
Para achar a tensão de cisalhamento e as tensões normais e , vamos substituir e nas equações de , e .
Com essas tensões, somos capazes de calcular no próximo passo!
Passo 3
Nesse passo a gente vai resolver a segunda parte do exercício, calculando e .
Vamos começar por , substituindo e na equação de .
Agora, vamos substituir , e na equação de para achar .
Eba! Achamos as duas densidades de energia de deformação específicas.
Passo 4
Nesse passo, vamos resolver a última parte da questão. Para isso, temos que igualar com !
Cortando dos dois lados da equação, achamos:
Era nessa equação que o enunciado pedia para a gente chegar! Ou seja: Uhuuul! Acabamos com a questão!