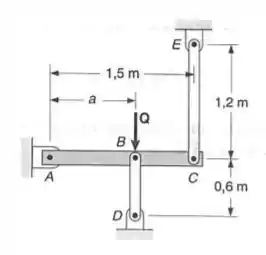
A barra rígida ABC é suportada por duas hastes de ligação BD e CE, de seção transversal retangular uniforme de e é feita de um aço doce, que é assumido ser elastoplástico com e . A intensidade Q de uma força aplicada em B cresce gradualmente desde zero até a deflexão em B atingir e então decresce até zero. Sabendo-se que , determinar:
- O máximo valor de Q e o correspondente valor da tensão normal em cada haste;
Passo 1
Fala galera, temos um exercício um pouco fora dos padrões que estamos acostumados, mas nada que seja muito assustador, na verdade, ele vai seguir alguns princípios que já conhecemos e alguns princípios novos que vamos ver. Como nosso objetivo são as tensões, vamos precisar das forças, e para isso, precisamos do nosso diagrama de corpo livre, assim teremos que:
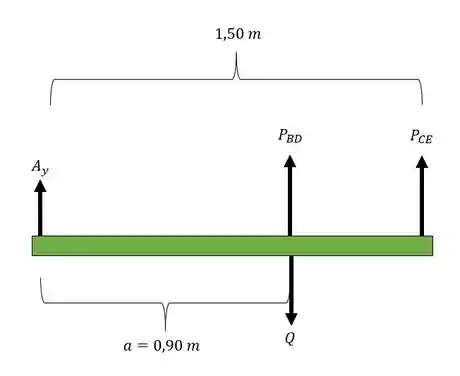
Porém, percebemos que temos um problema estáticamente indeterminado, porque temos duas incógnitas ( e uma equação , ou seja, precisamos de uma relação de deformações, montando um pequeno diagrama de deformações, temos que:
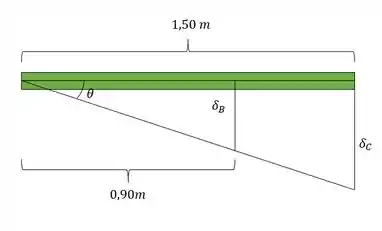
Assim podemos dizer que:
Porém, lembre-se que consideremos deformações muito pequenas, ou seja, tão pequenas que podemos fazer a seguinte aproximação:
Assim as deformações são consideradas da seguinte maneira:
Passo 2
Conseguimos uma relação para deformação fazendo uma análise geométrica no passo anterior, mas também temos que lembrar que podemos determinar a nossa deformação pela seguinte equação:
Como nosso objetivo é determinar as forças e com essas forças determinar a tensão, podemos usar essa equação anterior para determinar a força, e depois dividir ela pela área da seção para obter a tensão, assim, teremos que:
Sabemos que:
E como já sabemos a força, a tensão vai ser bem tranquila de calcular.
E tudo isso que fizemos na barra CE, poderemos fazer na barra BD, assim vamos ter que:
Sabemos que:
E como já sabemos a força, a tensão vai ser bem tranquila de calcular.
Passo 3
Agora que já temos as forças e as tensões, podemos trazer de volta a nossa equação de equilíbrio, assim, teremos que:
Isolando a carga atuante na nossa estrutura, teremos que:
E como já sabemos quanto cada uma dessas forças valem, podemos substitui-las, assim vamos ter que:
Agora vamos guardar essa fórmula porque já vamos usar ela, agora precisamos analisar as resistências das nossas barrinhas a partir das nossas tensões.
Passo 4
Sabemos que a tensão atuante na nossa barra BD é dada por:
E sabemos que a máxima tensão que age nela é a tensão de escoamento, exatamente por estarmos em um estado elastoplástico, assim, podemos admitir que a máxima tensão que pode atuar na nossa barra BD é dada por:
Se igualarmos os dois vamos ter o máximo ângulo para a barra BD, assim vamos ter que:
Assim a máxima deformação que a barra BD pode ter antes de escoar é dada por:
E perceba, como a deformação aplicada na nossa estrutura foi de temos que a deformação aplicada é maior que a deformação que a nossa barra BD poderia suportar, logo ela entrou em escoamento, assim, a máxima tensão atuante na nossa barra BD é a tensão de escoamento, assim vamos ter que:
Como a nossa barra entrou em escoamento, para determinar a força nela, basta fazermos o seguinte:
Passo 5
Sabemos que a tensão atuante na nossa barra CE é dada por:
E sabemos que a máxima tensão que age nela é a tensão de escoamento, exatamente por estarmos em um estado elastoplástico, assim, podemos admitir que a máxima tensão que pode atuar na nossa barra CE é dada por:
Se igualarmos os dois vamos ter o máximo ângulo para a barra CE, assim vamos ter que:
Assim a máxima deformação que a barra CE pode ter antes de escoar é dada por:
E podemos determinar a nossa deformação em C por regra de 3, assim teremos que:
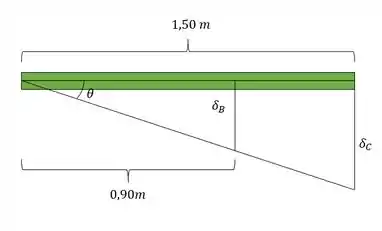
Ou seja, ela não ultrapassa a máxima deformação que a nossa barra poderia ter, desse modo temos como determinar o nosso ângulo que será dado por:
E a tensão na haste CE vai ser dada por:
Assim a carga de força será dada por:
Passo 6
Com a equação de equilíbrio podemos determinar a máxima carga Q
Sabemos que: