Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 56
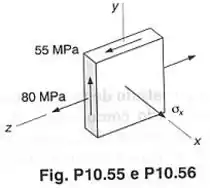
O estado de tensões mostrado ocorre em um componente de máquina, que é feito de um aço para o qual . Usando o critério da máxima energia de distorção, determinar a variação dos valores de , de tal modo que o coeficiente de segurança, em relação a tensão de escoamento, seja igual ou superior a .
Passo 1
Oi, galera bonita! Tudo na paz? Espero que sim! Sem enrolação, bora entender o que o resultado pediu e saber como resolver a questão!
O enunciado nos mostra uma figura com um estado de tensões e pede para a gente determinar quais os valores de fazem o coeficiente de segurança ser maior ou igual a , usando o critério da máxima energia de distorção. A figura abaixo mostra o estado de tensões do componente.
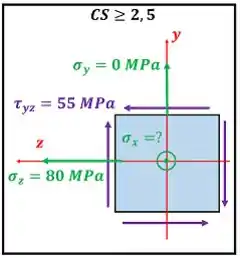
O critério da máxima energia de distorção usa as tensões principais , e .
O cálculo do coeficiente de segurança através desse critério é realizado, reorganizando a equação 10.36 do livro.
onde é a tensão de resistência ao escoamento do latão dada pelo enunciado . depende de .
Essa equação mostra que determinar os valores de que fazem é a mesma coisa que garantir que o lado esquerdo da inequação vai sempre ser menor ou igual ao lado direito.
Para garantir isso precisamos achar , e no próximo passo!
Passo 2
Para calcular as tensões principais , e , usaremos as equações de tensões principais abaixo, substituindo , , e da figura.
Agora estamos prontos para substituir as tensões principais na equação do critério de máxima energia de distorção e achar os valores de que queremos.
Passo 3
Vamos substituir , e na equação do critério de máxima energia de distorção e resolver a questão!
Vemos que a inequação acima é de segundo grau. Isso significa que, para encontrar os valores de que fazem o lado esquerdo permanecer menor ou igual a zero, precisamos achar as raízes através da fórmula de Bhaskara. Para usar essa fórmula, vamos reconhecer primeiro os valores dos coeficientes do polinômio de segundo grau.
Agora vamos substituir esses coeficientes na fórmula de Bhaskara.
Esses dois valores e são os limites de . Isso quer dizer que deve ficar na faixa de valores mostrados abaixo.
Aeeee! Terminamos a questão! Mandamos muito bem!