Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 62
O colar de é deixado cair de uma altura sobre uma placa presa na extremidade da barra vertical . Determinar:
- a máxima deflexão na extremidade ;
- a carga estática equivalente;
- a máxima tensão que ocorre na porção da barra.
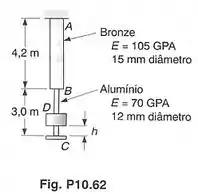
Passo 1
Oier, galerinha! Vamos exercitar nossos conhecimentos de resistência dos materiais fazendo uma questão de carregamento produzido por impacto?
A questão quer primeiro que a gente calcule a máxima deflexão que a barra pode ter sem danificar as barras e . Para elas não serem danificadas com essa deformação, a energia que elas recebem com o impacto deve ser igual a máxima energia de deformação que as barras podem aguentar juntas!
é a soma da energia que a barra absorve ao ser carregada com a máxima força possível com a energia que a barra absorve ao ser carregada com a máxima força possível . e são calculadas com a mesma equação 10.14 do livro.
onde e são os comprimentos das barras e respectivamente, e são as áreas das seções transversais das barras e respectivamente e e são os módulos de elasticidade das barras e respectivamente.
A energia que as barras absorvem com o impacto é a energia potencial que o bloco tem antes de cair de uma altura igual a .
onde é a massa do colar e é a aceleração da gravidade .
Substituindo na equação de , encontramos . Encontramos a partir da equação 10.3
do livro que calcula .
Por fim, o enunciado quer que a gente calcule a máxima tensão que ocorre na barra . Para calcular isso, basta dividir a máxima força pela área da barra!
A figura abaixo mostra os dados que temos para achar a deformação , a carga estática e a máxima tensão da barra .
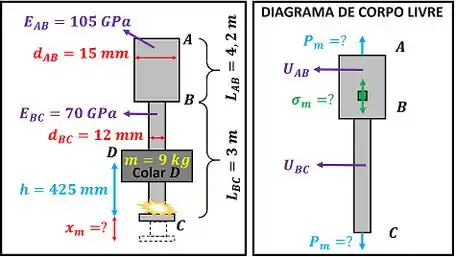
Com todas essas informações em mãos, vamos começar as contas.
Passo 2
Iniciamos os cálculos, pela letra (b) da questão. Vamos calcular primeiro o valor da carga estática equivalente da barra. Fazemos essa inversão, porque, para calcular o da letra (a) é necessário calcular da letra (b).
Para calcular temos que calcular .
Substituindo por esse valor de , achamos .
No entanto, antes disso precisamos converter e de para . Fazemos isso, multiplicando esses dois termos por .
Além disso, temos que calcular o valor das áreas e .
Agora sim somos capazes de achar , substituindo os dados na equação de .
Aeeee! Resolvemos a letra (b). Agora somos capazes de achar o que a letra (a) pede.
Passo 3
Achamos substituindo e na última equação oque aparece no passo 1.
Essa letra (a) foi rápida, né?
Então bora partir logo para a letra (c)!
Passo 4
Como dito no passo 1, calculamos a máxima tensão que ocorre na barra , dividindo a máxima força pela área da barra!
Dividindo esse valor em por , achamos o valor de em .
Uhuuuul! Achamos todas as respostas que a questão pedia!