Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 3

Para os estados de tensão mostrados nas figuras, determine as tensões normal e de cisalhamento que atuam na face oblíqua do elemento triangular sombreado na figura. Use um método de análise com base no equilíbrio daquele elemento, como foi feito nas deduções da seção 7.1 A .

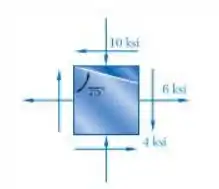
Passo 1

Fala aí, galerinha. Tudo bem com vocês? Bora estudar mecânica e garantir aquele notão na prova.

Este problema nos pede para determinarmos as tensões normal e de cisalhamento da figura. De acordo com a teoria que ele nos dá, se a área do triângulo é dada por A , as áreas das faces vertical e horizontal são respectivamente:

A cos ⁡ θ A sin ⁡ θ

Dado um novo eixo que passe pelas faces do triângulo, podemos escrever as seguintes equações de equilíbrio:

∑ F x ' = 0 σ x ' A + σ x A cos ⁡ θ sin ⁡ θ + τ x y A cos ⁡ θ cos ⁡ θ - σ y A sin ⁡ θ sin ⁡ θ - τ x y A sin ⁡ θ sin ⁡ θ = 0  

Onde as componentes x ' e y ’ são determinadas através do angulo   θ da face oblíqua e, através desta relação, podemos encontrar a tensão normal. Substituindo:

∑ F = 0 σ A + 4 A cos ⁡ 15 ° sin ⁡ 15 ° + 10 A cos ⁡ 15 ° cos ⁡ 15 ° - 6 A sin ⁡ 15 ° sin ⁡ 15 ° - 4 A sin ⁡ 15 ° sin ⁡ 15 ° = 0

σ = 10,93   k s i  

Passo 2

Para encontrarmos a tensão de cisalhamento, o processo é semelhante. Temos a seguinte relação:

∑ F y ' = 0 τ x ' y ' A + σ x A cos ⁡ θ cos ⁡ θ - τ x y A cos ⁡ θ s in ⁡ θ - σ y A sin ⁡ θ cos ⁡ θ - τ x y A sin ⁡ θ sin ⁡ θ = 0

Logo,

∑ F = 0 τ A + 4 A cos ⁡ 15 ° cos ⁡ 15 ° - 10 A cos ⁡ 15 ° sin ⁡ 15 ° - 6 A sin ⁡ 15 ° cos ⁡ 15 ° - 4 A sin ⁡ 15 ° sin ⁡ 15 ° = 0

τ = 0,536   k s i

É isso, galera.

Resposta

σ = 10,93   k s i

τ = 0,536   k s i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabe-se que existe um estado plano de deformação na superfície de um componente de máquina. Sabendo que E = 200 GPa e G = 77,2 GPa, determine a direção e a intensidade das três deformações específicas
Resolva o Problema 7.154 considerando que o extensômetro forma um ângulo β = 35 ° com um plano horizontal.
Resolva o Problema 7.152 considerando que o extensômetro forma um ângulo β = 35 ° com uma linha paralela ao centro do eixo.
O seguinte estado de deformação foi determinado na superfície de uma peça de máquina de ferro fundido: ϵ x = - 720μ ; ϵ y = - 400μ ; γ x y = 660μ Sabendo que E = 69 GPa e G = 28 GPa, determine os plan
O seguinte estado de deformação dado foi medido na superfície de uma placa fina. Sabendo que a superfície da placa está livre de tensão, determine ( a ) a direção e a intensidade das deformações princ