Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas de Revisão - Ex. 66
Na estrutura de aço mostrada na figura é utilizado um pino de 6 mm de diâmetro em C e são utilizados pinos de 10 mm de diâmetro em B e D. O limite da tensão de cisalhamento é 150 MPa em todas as conexões, e o limite da tensão normal é 400 MPa na barra BD. Sabendo que se deseja um coeficiente de segurança de 3,0, determine a maior carga P que pode ser aplicada em A. Note que a barra BD não é reforçada ao redor dos furos dos pinos.
Passo 1
Fala ai gurizada tudo bem?? Antes de começarmos a calcular, vamos esboçar nosso famoso diagrama de corpo livre do trecho ABC
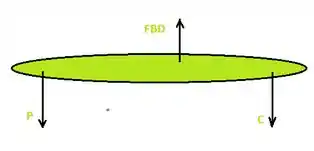
Primeiramente vamos começar calculando o somatório em C:
E agora o somatório em B:
Passo 2
Agora precisamos encontrar a tensão na seção do vinculo BD
(
Calculando o cisalhamento em B e C, temos:
(
Galera notem que o menor valor de é 3,9270 KN
Então podemos achar o P respectivo a este valor:
Passo 3
Então devemos encontrar o cisalhamento em C temos:
Então podemos achar o P respectivo a este valor:
Então percebemos que o menor valor de P é: 1,683 X
Resposta
P = 1,683 kN