Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas de Revisão - Ex. 69

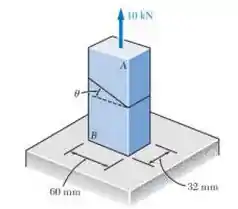
As duas partes do elemento AB são coladas ao longo de um plano formando um ângulo θ   com a horizontal. Sabendo que o limite de tensão para a junta colada é 17,24 MPa em tração e 8,96 MPa em cisalhamento, determine (a) o valor de θ para o qual o coeficiente de segurança do elemento seja máximo e (b) o valor correspondente do coeficiente de segurança. (Dica: equacione as expressões obtidas para os coeficientes de segurança respeitando a tensão normal e de cisalhamento).

Passo 1

Fala aí galera tudo certinho???? Antes de tudo vamos calcular a área da base do elemento do enunciado..

A 0 = 60   x   32 = 1920 m m 2 = 1920 × 10 ³ m ²

Considerando que o fator de segurança é igual para a tensão normal e de cisalhamento...

( F . S ) σ = ( F . S ) τ

Tensão normal: σ =   P A 0   c o s 2 θ   ∴   P U , σ =   σ U A 0 c o s 2 θ

Podemos deixar em evidencia o fator de segurança :D

( F . S . ) σ =   P U , σ P =   σ U A 0 P c o s 2 θ

Passo 2

A Tensão de cisalhamento é dada por:

τ =   P A 0 s e n θ c o s θ   ∴   P U , τ = τ U A 0 s e n θ c o s θ

Assim o fator de segurança para a tensão de cisalhamento temos:

( F . S . ) τ =   P U , τ P =   τ U A 0 P s e n θ c o s θ

Igualando:

σ U A 0 P c o s 2 θ = τ U A 0 P s e n θ c o s θ  

Assim temos:

a )   s e n θ c o s θ = t a n θ =   τ U τ U = 8,96 17,24 =   0,520

b) P U =   σ U A 0 c o s 2 θ = 12,5   x 1920 × 10 ³ c o s 2 27,5 ° = 3,05

F . S . = P U P = 3,05 10 = 0,30

Resposta

  1. θ o p t = 27,5 °
  2. F.S.= 0,30
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas placas de cobertura, cada uma com 12,7m m de espessura e 250m m de largura, são soldadas a uma viga de perfil laminado W 360 × 79 , como mostrado. Sabendo-se que uma força vertical P pode ser apl
Para a viga com o carregamento mostrado, determinar: (a) a seção transversal onde ocorre a máxima tensão normal; (b) a correspondente tensão normal máxima.
A força de 5k N é vertical, a força Q é horizontal, e ambas as forças atuam em planos perpendiculares ao eixo maciço A D . Sabendo-se que τ a d m = 45M P a , determinar o menor diâmetro permissível pa
Para a viga com o carregamento mostrado, determinar: (a) a seção transversal onde ocorre a máxima tensão normal; (b) a correspondente tensão normal máxima. Assumir h 12 h 0
O sistema eixo-engranagem mostrado está sujeito a um torque T A de 340N . m , enquanto que a polia D é mantida fixa. Sabendo-se que τ a d m = 70M P a , determinar o menor diâmetro permissível para o e