Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 78
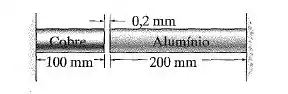
Os dois segmentos de haste circular, um de alumínio e outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de entre eles quando . Cada haste tem diâmetro de . , , , . Determine a tensão normal média em cada haste se . Calcule também o novo comprimento do segmento de alumínio.
Passo 1
Oláaaa, querido! Cê está bem? Vamos avaliar a situação que temos aqui!
Temos duas hastes presas, mas elas não se encostam. Mas com o aumento de temperatura, elas irão sofrer expansão térmica, e vão crescer de comprimento e passarem a se tocar.
Aí uma começa a aplicar uma força na outra, já que ambas querem se expandir além do espaço disponível. Isso gera uam tensão nas duas hastes.
Características da haste de cobre:
- Cobre: , .
- Comprimento inicial: .
- Alumínio: , .
- Comprimento inicial: .
Características da haste de alumínio:
A temperatura inicial nas duas hastes é .
As hastes estão presas em paredes rígidas, e há uma folga de entre elas.
Quando as hastes esquentarem, elas irão expandir. Quando a temperatura chegar em , queremos saber qual é a tensão em cada haste e qual o novo comprimento da haste de alumínio. Bora!
Passo 2
Vejamos o que acontece com cada haste:
- O aumento de temperatura vai causar uma expansão das hastes. Então a haste de cobre vai ser alongar e a haste de alumínio vai ser alongar
- As hastes vão se encostar, aí cada haste que quer se expandir vai forçar a outra, comprimindo essa outra com uma força . Essa força tende a reduzir as hastes. Então a haste de cobre vai ter um encurtamente e a de alumínio um encurtamento de
As paredes são fixas (rígidas), então o resultado aí de toda essa mudança de comprimento (expansão e compressão em cada haste) tem que ser o tamanho da folga!
Temos que escrever uma equação com isso tudo. A haste de cobre expande ( e reduz () . A haste de alumínio expande ( e reduz () . A soma dos totais é igual ao comprimento da folga:
Passo 3
Temos fórmulas pra todos esses termos! Percebe que a expansão das hastes acontece por causa da mudança de temperatura, então vamos usar a fórmulinha do alongamento por temperatura:
E a compressão das hastes vai ser causada pela força que uma haste exerce sobre a outra. Então vamos usar a relação carga-deslocamento:
Nós queremos a tensão em cada haste. Vamos substituir logo a fórmula dela na equação acima pra deixar tudo pronto pra aplicar. Temos
Substituindo na equação de cima:
Então os encurtamentos são dados por
Beleza! Temos um jeito de chegar até a tensão.
Passo 4
Vamos aplicar as fórmulas. A variação térmica foi .
Então a expansão da haste de cobre foi:
E a da haste de alumínio:
Passo 5
Agora vamos usar a relação carga-deslocamento.
Vamos parar para pensar um pouco. As hastes tem o mesmo diâmetro, então a área delas é igual. E a força que a haste de alumínio exerce na de cobre vai ser a força que essa haste de cobre recebe por causa da lei de ação e reação.
Como a tensão depende da área e da força aplicada, as tensões nessas duas hastes vão ser iguais:
Logo, podemos calcular o encurtamente da haste cobre assim:
E da haste de alumínio:
Passo 6
Voltando à condição de compatibilidade:
Substituindo o que a gente achou aí e simplificando:
Isolando :
Passo 7
A questão também pede o novo comprimento da haste de alumínio. Ela vai sofrer expansão térmica e vai encurtar por causa da força. Então o comprimento final dela é:
Já calculamos todos esses , agora é substituir:
Resposta
.