Para a estrutura do Prob. 11.39, determinar(a) a distância h para que o coeficiente de segurança, em relação a flambagem, seja o mesmo para cada um dos dos quatro membros;(b) a correspondente tração admissível no membro AC, se o coeficiente de segurança é 2,8.

Passo 1
Fala aí, bora analisar essa estrutura?
Precisamos encontrar a altura que otimize o coeficiente de segurança das 4 barras, pra facilitar nossa vida as barras horizontais são simétricas e as verticais também então precisaremos analisar só duas e faremos para BC e CD. A barra AC será tracionada então ela não sofre flambagem, porém a tração nela puxar e comprimir outras barras e é ai que a gente vai analisar a flambagem. Vamos desenhar o nó C e analisar o equilíbrio.
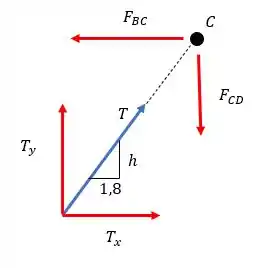
E com isso faremos os esforços em cada barra serem relacionados ao peso admissível e ao fator de segurança que tem a seguinte relação:
Lembrando que pro peso crítico é dado por:
Vamos então calcular para cada barra o respectivo peso admissível, porém antes acharemos uma relação entre a tração e o esforço em cada barra.
Passo 2
Como prometido vamos encontrar as relações com T, fazendo o somatório das forças no nó C:
E pela figura a gente calcula o comprimento da barra e as relações com as decompostas:
Daí podemos dizer que:
Daí:
E pelo somatório das forças horizontais temos:
E pela figura:
Então:
Passo 3
Bacana, encontrados os esforços podemos pensar o seguinte se essas barras resistem a flambagem com o coeficiente de segurança desejado temos que:
Então vamos ao cálculo do peso crítico.
E precisamos do momento de inércia que nesse caso será calculado em m
E da figura a gente vê que o comprimento da barra BC é:
Substituindo temos:
Daí voltando ao peso admissível:
E como vimos que:
Podemos substituir.
e isolar :
Daí:
Passo 4
Ainda não acabou por aí, precisamos avaliar a outra barra e faremos como no passo 3.
Então vamos ao cálculo do peso crítico.
E o momento de inércia é o mesmo pois as barras possuem o mesmo diâmetro, porém no inicio nós fizemos uma relação em metros e aqui no peso crítico vai aparecer uma incógnita que também precisa estar em metros.
Substituindo temos:
Aqui usamos o módulo de elasticidade em e encontramos uma unidade compatível com a encontrada no último passo.
Daí voltando ao peso admissível:
E como vimos que:
E igualando os termos temos:
E aí isolando o fator:
Passo 5
Beleza, chegamos juntos até aqui e o fator de segurança é o mesmo para as duas barras, sendo assim igualamos as equações encontradas:
Eliminando os termos iguais temos:
Agora isolando .
Passo 6
E para o item b. como temos o mesmo fator de segurança para ambas as barras podemos pegar qualquer uma das expressões encontradas:
Isolando T:
Substituindo os valores: