Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 37
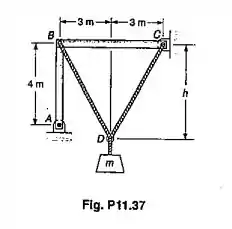
Os membros articulados AB e BC consistem de tubos de alumínio, cujas seções tem 120mm de diâmetro externo e 10mm de espessura. Sabendo-se que um coeficiente de segurança de 3,5 é desejado, determinar a maior massa m do bloco, que pode ser suportado pelo arranjo mostrado, quando h=4m. Usar E=70GPa e considerar somente a flambagem no plano da estrutura.
Passo 1
Fala aí, pediu outra questão de flambagem com coeficiente de segurança?
Nossa situação é a seguinte, temos que calcular a massa do bloco para a estrutura resistir a flambagem com um coeficiente de segurança, a gente vai ter que observar como o cabo se comporta transferindo para a estrutura das barras e decompor alguns esforços aqui, ok?
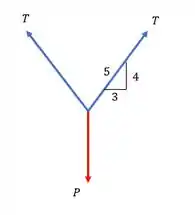
Desenhando o DCL dos cabos a gente pode relacionar o esforço de tração nos cabos T, com o peso P do bloco e depois disso poderemos relacionar com o peso admissível de cada coluna e a gente pode ver no DCL como isso vai ficar:
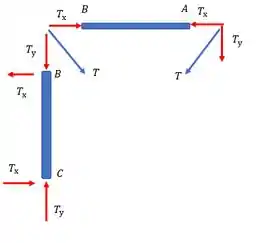
Após isso vamos relacionar cada esforço desses nas barras com o peso admissível dado por:
Lembrando que pro peso crítico é dado por:
Passo 2
Vamos as relações que a gente precisa, a primeira é no cabo. Se a gente olhar o triângulo na figura vai ficar bem fácil a decomposição. Vamos fazer o somatório dos esforços no cabo para achar uma relação de P.
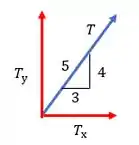
Assim o somatório das forças fica para os dois cabos:
A gente tira então que:
E será o peso que vai causar flambagem na barra vertical, e um jeito beeem fácil de acharmos a relação de com o peso é através do próprio da figura a gente pode tirar a seguinte relação:
Então:
Passo 3
Agora sim vamos fazer aquelas relações que queríamos, vamos dizer que para o fator de segurança desejado a relação deve ser respeitada:
Que no caso faz a barra AB resistir á flambagem com segurança e lembrando que:
E para esse tipo de barra o momento de inércia é:
Substituindo os valores, temos.
E substituindo na fórmula para :
E como:
E aqui a massa pode ser calculada por:
E substituindo
Passo 4
Ainda é necessário avaliar P para a barra AB, faremos o mesmo processo:
Que no caso faz a barra AB resistir á flambagem com segurança e lembrando que:
O momento de inércia já foi calculado antes e vale:
Substituindo os valores, temos.
E substituindo na fórmula para :
E como:
Temos:
Como esse é o menor dos pesos, tomamos ele como o máximo que a estrutura pode suportar e aí:
Tomando