Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 41
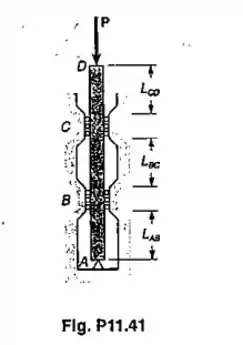
Uma coluna quadrada de alumínio, de 25mm de lado, é mantida na posição mostrada,
por um pino em A e por uma série de roletes em B e C, que impedem a rotação da coluna no
plano da figura, Sabendo-se que Lab=0,9m, Lbc=1,2m e Lcd=0,3m, determinar a carga
admissível P, usando um coeficiente de segurança em relação a flambagem de 3,2. Considerar somente flambagem no plano da figura e usar E=77GPa.
Passo 1
Fala pessoal, bora analisar mais uma estrutura?
Esse exercício traz pra gente o conceito de coeficiente de flambagem e ele vai entrar no comprimento efetivo do peso crítico:
E o peso crítico alterado fica:
Bom o nosso problema é um pouco diferente dos que temos visto, essa coluna tem vários travamentos e a chave pra resolver a questão é justamente os tipos de travamento. Foi dito que os roletes travam a rotação então funcionam como engaste, já o pino em A permite o giro, vamos desenhar as deformações e definir para cada trecho um coeficiente de flambagem.
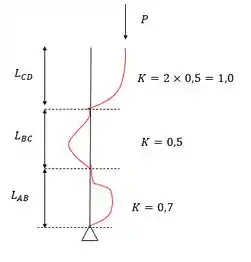
Esses coeficientes foram retirados das tabelas de deformadas, para o trecho CD há rolete que funciona como engaste daí a coluna trabalha como engastada e livre. O trecho BC é engastado nas duas extremidades, enquanto o trecho AB é engastado e rotulado.
Passo 2
Vamos calcular o peso crítico para cada trecho e avaliar o menor dos 3 vai ser o que a gente procura. Antes precisamos do momento de inércia que é constante por toda a coluna.
E bora pro peso crítico, começando pelo trecho CD, que possui comprimento:
E:
E aí:
Então:
Para o trecho BC o comprimento é:
E:
E aí:
E para o trecho AB:
E o coeficiente de flambagem:
Daí:
E esse como foi o menor é o peso crítico que vamos usar para o admissível.
Passo 3
Agora é só partir para o abraço, lembrando que:
E com