Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 16b
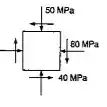
Para o estado de tensões dado, determinar as tensões, normal e de cisalhamento, depois que o elemento mostrado tenha sofrido uma rotação de:(b) 15 no sentido horário
Passo 1
E aí, bora resolver mais um exercício?
Esse tipo de problema a gente resolve usando o famoso círculo de Mohr, vamos começar calculando o centro:
A gente precisa do centro pra encontrar no círculo o ponto que a questão nos deu, pra isso vou te dar uma dica maneirinha que é: quando o elemento for girado em um sentido, de um ângulo qualquer, a gente vai girar o dobro do ângulo no sentido contrário.
Passo 2
Agora que encontramos o centro, a gente vai calcular o ângulo e o raio do círculo. Para isso vale fazer um desenho pra dar uma facilitada.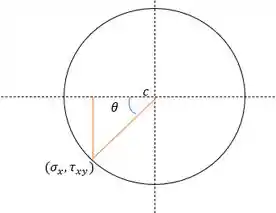
Daí a gente retira esse triângulo retângulo e faz as relações necessárias.
Nesses casos é uma boa ideia calcular o ângulo usando um módulo e olhando pra figura desenhada.
Como é a medida vertical, a gente pode tirar daqui que:
Passo 3
Show de bolinhas, agora vamos colocar em prática o macete. A gente viu que o elemento é girado de 15 graus no sentido horário, vamos girar 30 graus no sentido anti-horário no círculo e encontrar as tensões que a gente quer.
Ou seja, agora o novo ponto está girado de 99,44 graus no sentido anti-horário a partir do segundo quadrante. O referencial do círculo deve ser a partir do eixo x no sentido anti-horário e no primeiro quadrante, para não errarmos os sinais das tensões, sendo assim: