Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 23a

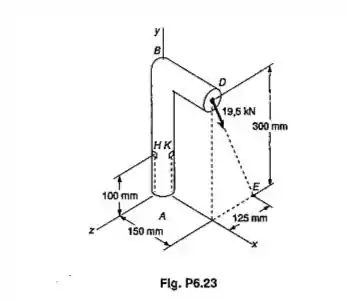
Uma força de 19,5kN é aplicada no ponto D da barra de ferro fundido mostrada. Saendo-se que a barra tem um diâmetro de 60mm, determinar as tensões principais e a máxima tensão de cisalhamento no:(a) ponto H;(b) ponto K.

Passo 1

E aí, bora matar mais uma questão?

Vamos começar decompondo a força no ponto D, nas direções y e z.

D E = 125 2 + 300 2 = 325 m m

F y = - 300 325 × 19,5 = - 18 k N

F z = - 125 325 × 19,5 = - 7,5 k N

Com isso podemos calcular os momentos na seção e analisar nossos pontos.

M x = - 7,5 × 300 - 100 = - 1500 k N . m m

M Y = 7,5 × 150 = 1125 k N . m m

M Z = - 18 × 150 = - 2700 k N . m m

Passo 2

Vamos calcular as propriedades geométricas:

A = π d 2 4 = 2827,88 m m ²

J = π r 4 2 = 1,272 × 10 6 m m 4

I = J 2 = 636,172 × 10 3 m m 4

E o momento estático de um semicírculo:

Q = 2 3 r 3 = 18 × 10 3 m m 3

t = d = 60 m m

c = r = 30 m m

Passo 3

Enfim para o ponto H, teremos as tensões:

σ = F y A - M x c I

σ = - 18 × 10 3 2827,88 - ( - 1500 × 10 3 × 30 )   636,172 × 10 3 = 64,37 M P a

τ = F x Q I t + M y c J

τ = 0 + 1125 × 10 3 × 30   1,272 × 10 6 = 26,533 M P a

Passo 4

Vamos colocar esses valores no círculo de Mohr e ver o que a gente consegue tirar.

σ y = 67,37 M P a

σ x = 0

τ x y = 26,533 M P a

E com isso:42

c = ( σ x + σ y ) 2 = 32,19 M P a

Lembrando que:

τ m á x = R = σ x - c 2 + τ x y 2 = 41,7 M P a  

E enfim:

σ 1 = c + r = 73,9 M P a

σ 2 = c - r = - 9,51 M P a

Resposta

σ 1 = 73,9 M P a

σ 2 = - 9,51 M P a

τ m á x = 41,7 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento mostrado, determinar: (a) a seção transversal onde ocorre a máxima tensão normal; (b) a correspondente tensão normal máxima.
A força de 5k N é vertical, a força Q é horizontal, e ambas as forças atuam em planos perpendiculares ao eixo maciço A D . Sabendo-se que τ a d m = 45M P a , determinar o menor diâmetro permissível pa
Para a viga com o carregamento mostrado, determinar: (a) a seção transversal onde ocorre a máxima tensão normal; (b) a correspondente tensão normal máxima. Assumir h 12 h 0
O sistema eixo-engranagem mostrado está sujeito a um torque T A de 340N . m , enquanto que a polia D é mantida fixa. Sabendo-se que τ a d m = 70M P a , determinar o menor diâmetro permissível para o e
Para a viga com o carregamento mostrado e usando os dados abaixo, determinar: (a) a seção transversal onde ocorre a máxima tensão normal; (b) a maior varga distribuída w que pode ser aplicada. Dados: