Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 11
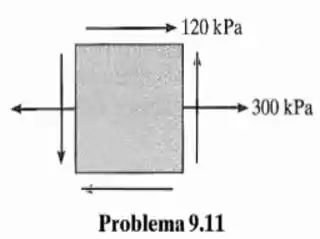
11. Determine o estado de tensão equivalente em um elemento, se ele estiver orientado a em sentido horário em relação ao elemento mostrado
Passo 1
Se liga só! A coisa mais importante desse problema é identificar as tensões correspondentes ao estado plano! Um erro aqui é fatal! Eu disse , hein!?
Fazendo a identificação correta, é só usar as formulinhas já prontas pra determinar as tensões quando o elemento está orientado em um dado ângulo, no nosso caso, o de .
Pois muito bem! Bora pro que interessa!
Olhando a figura do enunciado, tiramos do estado plano de tensão que...
Passo 2
Bom! A questão pede que a gente determine o estado de tensão e nesse elemento, caso os seus eixos sejam rotacionados por um ângulo de no sentido horário .
Portanto, já sabe né!? Em ResMat, sentido horário remete ao lado negativo da força.
Ou seja, nosso ângulo vai ter um valor negativo.
Vamos então, aplicar as fórmulas de transformação de tensão que já conhecemos, para encontrar nossa resposta:
E como sabemos o valor das seguintes variáveis...
Só nos resta substituir esses valores nas três expressões das tensões acima, para encontrar quanto vale cada uma...
Onde encontramos então, que:
Passo 3
Pra finalizar! Porque não, obtidas essas tensões, fazer um esboço delas no elemento rotacionado.
Sabemos que a tensão no eixo , por ter dado negativa, é de compressão e a tensão no eixo , com valor positivo, é de tração.
E sabemos também, que como deu positivo; as setas de tensão cisalhante no nosso esqueminha irão convergir para o e quadrantes.
Assim, já podemos imaginar mais ou menos a cara do nosso elemento! Pra finalizar, só falta sua orientação!
Ihhh rapaz! É mesmo! O próprio enunciado diz que ele está orientado no sentido horário!
Então, já não falta mais nada pra esboçar o nosso circuito!
E chegamos então, até a seguinte figura abaixo...
