Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 86

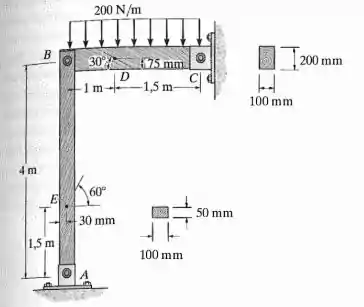
A estrutura suporta a carga distribuída de 200 N/m. Determine a tensão normal e a tensão de cisalhamento no ponto E que agem nos sentidos perpendicular e paralelo às fibras, respectivamente. Nesse ponto, as fibras formam um ângulo de 60º com a horizontal, como mostra a figura.

Passo 1

Primeiramente, vamos calcular os esforços atuantes:

∑ M a = 0 → - 500 × 1,25 + 2,5 F c = 0

F c = 250 N

F a = 500 - 250 = 250 N

∑ F y = 0 → 250 - N = 0

N = 250 N

Logo, as tensões em E serão:

σ E = - N A = - 250 0,05 × 0,1 = - 50 k P a

τ E = V Q I t = 0

Passo 2

Logo, podemos calcular a tensão média e o raio do círculo de Mohr:

σ m é d = - 50 2 = - 25 k P a

R = 25 ² = 25 k P a

Por fim, as tensões no ponto dado serão:

σ x ' = - 25 + 25 cos ⁡ 60 ° = - 12,5 k P a

τ x ' y ' = 25 s e n 60 ° = 21,7 k P a

Resposta

σ x ' = - 12,5 k P a

τ x ' y ' = 21,7 k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A manivela do pedal de uma bicicleta tem a seção transversal mostrada na figura. Se ela estiver presa à engrenagem em B e não girar quando submetida a uma força de 400 N, determine as tensões principa
A estrutura suporta a carga distribuída de 200 N/m. Determine a tensão normal e a tensão de cisalhamento no ponto D que agem nos sentidos perpendiculares e paralelos às fibras, respectivamente. Nesse
Os degraus da escada rolante estão apoiados nos dois lados pelo pino móvel em A e pelo rolete em B. Se um homem que pesa 1.500 N (~150 kg) estiver em pé no centro do degrau, determine as tensões princ
A barra retangular em balanço está sujeita à força de 25 kN. Determine as tensões principais no ponto A.