Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 81

A barra retangular em balanço está sujeita à força de 25 kN. Determine as tensões principais no ponto A.

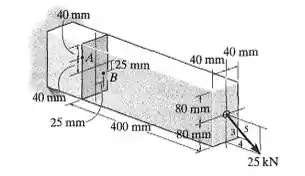
Passo 1

Primeiramente, calculando os esforços na peça, teremos.

N = 25 × 4 5 = 20 k N

V = 25 × 3 5 = 15 k N

M = 15 × 0,4 = 6 k N m

Logo, calculando-se as tensões em A:

σ a = N A + M c I = 20 × 10 3 0,08 × 0,16 + 6 × 10 3 0,04 0,08 × 0,16 3 12 = 10,35 M P a T

τ a = V Q I t = 15 × 10 3 0,06 × 0,08 × 0,04 0,08 × 0,16 3 12 0,08 = 1,32 M P a

Passo 2

O próximo passo é calcular a tensão média e o raio do círculo:

σ m é d = 10,35 2 = 5,175 M P a

R = 5,175 2 + - 1,32 2 = 5,34 M P a

Logo, podemos calcular as tensões principais:

σ 1 = 5,175 + 5,34 = 10,52 M P a

σ 2 = 5,175 - 5,34 = - 0,165 M P a

Resposta

σ 1 = 5,175 + 5,34 = 10,52 M P a

σ 2 = 5,175 - 5,34 = - 0,165 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 10.7 usando o círculo de Mohr.
As componentes da deformação em um ponto são ε x = - 480 ( 10 - 6 ) , ε y = 650 ( 10 - 6 ) , γ x y = 780 ( 10 - 6 ) e ε z = 0 . Determine (a) as deformações principais, (b) a deformação por cisalhamen
A roseta de deformação a 45° está montada sobre uma chapa de alumínio. As seguintes leituras foram obtidas para cada extensômero: ∈ a = 475 × 10 - 6 ;∈ b = 250 × 10 - 6 e ∈ c = - 360 × 10 - 6 . Determ
A barra de aço está sujeita à carga de tração de 2,5 kN. Se tiver 12 mm de espessura, determine a deformação por cisalhamento máxima absoluta. E = 200 G P a e v = 0,3 .
(a) Prove que a expressão σ x ' σ y ' - τ x ' y ' 2 , onde σ x ' , σ y ' e τ x ' y ' são componentes da tensão ao longo dos eixos retangulares x ' e y ' , independe da orientação destes eixos. Também