Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 83

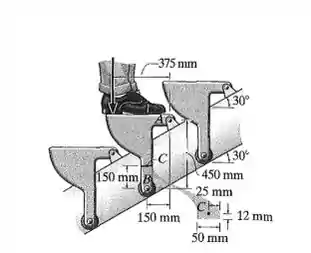
Os degraus da escada rolante estão apoiados nos dois lados pelo pino móvel em A e pelo rolete em B. Se um homem que pesa 1.500 N (~150 kg) estiver em pé no centro do degrau, determine as tensões principais desenvolvidas na seção transversal no ponto C. Os degraus movem-se à velocidade constante.

Passo 1

Primeiramente, vamos determinar as reações:

∑ M a = 0 → 1500 × 0,375 - 2 F s e n 60 ° 0,45 = 0

F = 792,47 N

∑ F x = 0 → V - 396,235 = 0

V = 396,235 N

∑ F y = 0 → 686,3 - N = 0

N = 686,3 N

∑ M = 0 → M - 396,235 × 0,15 = 0

M = 59,435 N

Passo 2

Agora, vamos calcular as tensões:

σ c = - N A = - 686,3 0,012 × 0,05 = - 1,1438 M P a C

τ c = V Q I t = 396,235 0,0125 × 0,025 × 0,012 0,012 0,012 × 0,05 3 12 = 0,9906 M P a

Calculando-se a tensão média, que será o centro do círculo:

σ m e d = 0 - 1,1438 2 = - 0,572 M P a

Calculando também o raio:

R = - 0,572 2 + 0,9906 2 = 1,1439 M P a

Logo, podemos calcular as tensões principais:

σ 1 = 1,1439 - 0,572 = 0,572 M P a

σ 2 = - 1,1439 - 0,572 = - 1,716 M P a

Resposta

σ 1 = 1,1439 - 0,572 = 0,572 M P a

σ 2 = - 1,1439 - 0,572 = - 1,716 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 10.5 usando o círculo de Mohr.
As componentes da deformação no ponto A sobre a aba da cantoneira são ε x = - 140 ( 10 - 6 ) , ε y = 180 ( 10 - 6 ) , γ x y = - 125 ( 10 - 6 ) e ε z = 0 . Determine (a) as deformações principais em A,
As componentes da deformação no ponto A sobre o suporte são ε x = 300 ( 10 - 6 ) , ε y = 550 ( 10 - 6 ) , γ x y = - 650 ( 10 - 6 ) , ε z = 0 . Determine (a) as deformações principais em A, (b) a defor
Resolva o Problema 10.9 usando o círculo de Mohr.
Resolva o Problema 10.6 usando o círculo de Mohr.