Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 17
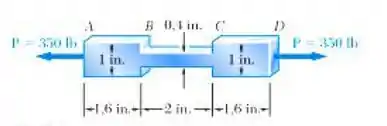
O sólido mostrado foi cortado de uma chapa de vinil com in de espessura e é submetido a uma tração de 350 lb. Determine (a) a deformação total do sólido, (b) a deformação de sua porção central BC.
Passo 1
E aí gurizada tudo belezinha???? Espero que sim !! na alternativa A o exercício pede a deformação total do sólido, notem que AB= CD , então para facilitarmos os cálculos vamos apenas fazer em AB e também na seção BC, vejam que é só aplicação na equação :D
.
Como te falei anteriormente as seções AB= CD então consideramos....
.
Então para o cálculo da deformação total basta somarmos todas as deformações ....
- Deformação total:
- Deformação da porção BC, já calculamos e o valor é:
Resposta
Exercícios de Livros Relacionados
O raio original do tubo curvado é 0,6 m . Se ele sofrer aquecimento não uniforme que provoque uma deformação normal ao longo de seu comprimento ∈ = 0,05 cos θ , determine o aumento no comprimento do
Um cabo fino é enrolado ao longo da superfície cuja forma é y =0,02x², onde x e y são dados em mm. A posição original da extremidade B é x = 250 mm. Se o cabo sofrer uma deformação normal∈ = 0,0002x a
A fibra A B tem comprimento L e orientação θ . Se suas extremidades A e B sofrerem deslocamentos muito pequenos u A e v B , respectivamente, determine a deformação normal na fibra quando ela estiver n
Um corpo de prova com comprimento original de 300m m tem diâmetro original de 12m m e é submetido a uma força de 2,5k N . Quando a força é aumentada para 9k N , o corpo de prova sofre um alongamento d
Um elemento estrutural de um reator nuclear é feito de uma liga de zircônio. Se esse elemento tiver se suportar uma carga axial de 20k N , determine a área da seção transversal exigida. Use um fator d