Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 34
A fibra tem comprimento e orientação . Se suas extremidades e sofrerem deslocamentos muito pequenos e , respectivamente, determine a deformação normal na fibra quando ela estiver na posição ’.
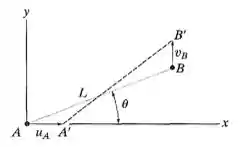
Passo 1
Oláaa! Essa questão é mais geométrica do que de resmat, então segura na minha mão. Vamos conseguir!
Queremos a deformação normal em , certo? Então a gente precisa do comprimento inicial de e o final. Aí é só usar a fómulinha dessa deformação:
O enunciado já diz que o comprimento inicial é
Precisamos achar então o comprimento final. Bora lá!
Passo 2
Se a gente decompor nos eixos coordenados, ficamos com algo assim:
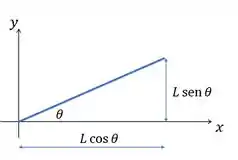
Aí comparando isso, com os deslocamentos de e :
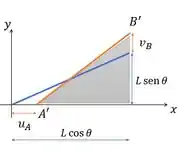
A gente consegue achar o comprimento de usando Pitagoras:
Passo 3
Logo:
Resposta
Exercícios de Livros Relacionados
O estado plano de tensões mostrado é conhecido na superfície de um componente de máquina, feito de aço de alta resistência. Sabendo-se que E = 200G P a e G = 80 G P a , determinar a orientação e a int
O estado plano de tensões mostrado é conhecido na superfície de um componente de máquina, feito de aço de alta resistência. Sabendo-se que E = 200G P a e G = 80 G P a , determinar a orientação e a int
Para o dado estado plano de deformação, usar o método da S e c .6.10 para determinar o estado de deformação associado aos eixos x ’ e y ’ , que foram girados de um ângulo θ , no sentido mostrado. ε x
Para o dado estado plano de deformação, usar o método da S e c .6.10 para determinar o estado de deformação associado aos eixos x ’ e y ’ , que foram girados de um ângulo θ , no sentido mostrado. ε x
Para o dado estado plano de deformação, usar o método da S e c .6.10 para determinar o estado de deformação associado aos eixos x ’ e y ’ , que foram girados de um ângulo θ , no sentido mostrado. ε x