Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 5
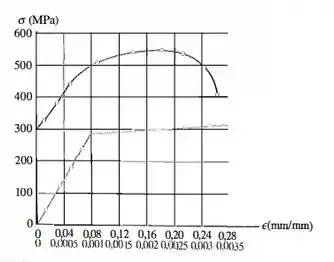
A figura apresenta o diagrama tensão-deformação para um aço-liga com de diâmetro original e comprimento de referência . Determine os valores aproximados do módulo de elasticidade para o material, a carga aplicada ao corpo de prova que causa escoamento e a carga máxima que o corpo de prova suportará.
Passo 1
Falaaaa! Tá bem?
A gente tem um cilindro sofrendo uma carga crescente. Esse gráfico relaciona a tensão normal no cilindro com a deformação longitudinal que ele sofreu.
Vamos entender melhor esse gráfico aí. A curva de baixo é o começo do diagrama. E a de cima é a continuação, para tensões maiores. Os dois representam o mesmo material, beleza? Se a gente fosse arrumar mais bonitinho, de forma aproximada, ele seria assim
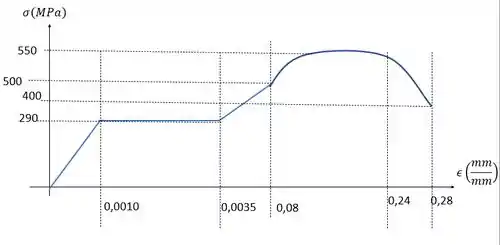
Queremos módulo de elasticidade para o material, a carga aplicada ao corpo de prova que causa escoamento e a carga máxima que o corpo de prova suportará. E esse gráfico vai nos ajudar dando alguns dados para isso.
Bora achar esses bonitos!
Passo 2
Primeiro, vamos calcular o módulo de elasticidade.
Para isso, devemos saber que ele é dado pelo coeficiente angular da primeira reta que forma o gráfico que a gente tem (tensão-deformção).
Como ela sai da origem, a gente precisa dividir um valor de pelo seu valor de , desde que o ponto esteja nessa primeira reta que vai até .
Vamos então pegar os pontose . Fica assim:
Passo 3
Queremos obter a carga aplicada ao corpo de prova quando ele chega na tensão de escoamento, ou seja , a carga que causa . Para isso, temos que calcular a área da seção, que é uma área circular. Logo, é dada por:
E por que a gente precisava dessa área ein? Porque a gente pode substituir nossos valores na fórmula da tensão normal e isolar :
Passo 4
Por último, ele pede a carga máxima que corpo suportará.
Vamos fazer algo bem parecido ao passo anterior. Pelo gráfico, a tensão máxima que ele suporta é . E como a gente sabe a área da seção do corpo de prova, podemos achar a carga usando a fórmulinha de tensão normal novamente: