Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 33
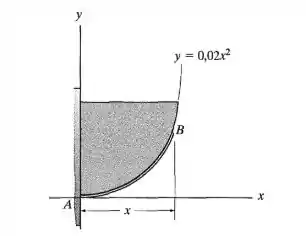
Um cabo fino é enrolado ao longo da superfície cuja forma é y =0,02x², onde x e y são dados em mm. A posição original da extremidade B é x = 250 mm. Se o cabo sofrer uma deformação normal = 0,0002x ao longo de seu comprimento, determina mudança no comprimento do cabo. Dica: Para a curva y = f(x), ds =
Passo 1
Olá, queridão! Tá bem?
Então, não se assusta com essas funções e tudo mais, vamos com calma e conseguir resolver essa juntos.
Primeiro, ele diz que o cabo está enrolado nessa superfície e vai até . Então se a gente for desenhar só ele no plano, seria algo assim:
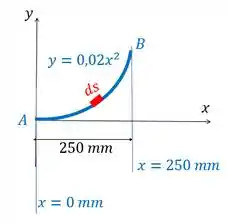
Percebe que ele começa em e termina em . E a gente marcou ali um pedacinho desse cabo, de comprimento (um comprimento beeem pequeno).
Aí ele diz que o cabo sofre uma deformação normal que vale e pede o quando o comprimento do cabo variou.
Bora ver como achar isso!
Passo 2
Então, cara, se a gente tivesse um cabo reto de comprimento inicial e a gente disse que ele teve uma deformação de , a variação de comprimento desse cabo seria:
Na nossa situação vamos ter algo parecido. Só que nosso cabo não está reto. E aí o que muda? Bem, a gente pode olhar só um pedacinho do nosso cabo. Esse pedacinho é tão pequeno, que podemos considerar que ele é reto.
Lembra do comprimento desse pedacinho? A gente disse que . E como o cabo sofre uma deformação , esse pedacinho do cabo também sofre essa deformação.
Então se a gente fosse escrever essa variação bem pequena no comprimento desse pedacinho , seria:
Passo 3
Mas não para por aí! Ele diz que para , ou seja, para um cabo dado por uma função , o comprimento de um pedacinho desse cabo , é dado por:
Onde é a derivada de . No nosso caso, o cabo é dado por
Então a derivada fica:
E nosso fica:
E aí o alongamento do nosso pedacinho fica:
Passo 4
A gente tem a variação de comprimento de um pedacinho do nosso cabo. Para saber a variação de comprimento do cabo todo precisamos somar essa variação para cada pedaço que compõem o cabo. Como? Integrando!
Percebe que a gente integrou de a porque nosso cabo está dentro desse intervalo de , e deve ser dado em .
Aí temos uma integral para resolver. Bora usar essa substituindo simples:
Usando essa substituição e calculando, vamos ter: