Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 31
A figura mostra a porção elástica do diagrama tensão – deformação de cisalhamento para um aço – liga. Se um parafuso de de diâmetro feito desse material for utilizado em uma junta sobreposta, determine o módulo de elasticidade e a força exigida para provocar o escoamento do material. Considere .
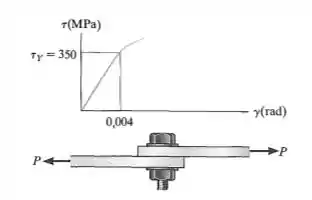
Passo 1
Desejamos encontrar o módulo de elasticidade e a força que vai provocar o escoamento do nosso material, dado o coeficiente de Poisson. Através do gráfico podemos encontrar o módulo de rigidez que é nada mais nada menos que o coeficiente angular da reta dada na imagem, assim
Essa grandeza vai se relacionar com nosso módulo de elasticidade através da seguinte fórmula
Passo 2
Tendo em mãos os valores de e podemos encontrar o módulo de elasticidade através da fórmula acima, assim
Do diagrama, podemos ainda utilizar o valor da tensão e através da equação da tensão de cisalhamento encontrar quanto vale fazendo
Onde e, então, obtemos