Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 64

Uma força de tração de 2,75   k N é aplicada a um corpo de prova feito de placa de aço plana de 1,6   m m ( E = 200   G P a ,       v = 0,30 ) . Determine a variação resultante (a) no comprimento de referência de 50   m m , (b) na largura da parte AB do corpo de prova, (c) na espessura da parte AB e (d) na área da seção transversal da parte AB.

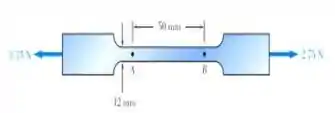
Passo 1

Fala aí gurizada tudo belezinha? Para Determinarmos a variação resultante no comprimento primeiramente devemos determinar a área, vem comigo :D

A = 1.6   x   12 = 19,20 m m 2 = 19,20   x   10 - 6   m 2 Sabendo que P = 2,75   x   10 - 6 m 2 , temos que então determinarmos a tensão: σ x = P A = 2,75   x   10 3 19,20   x   10 - 6 = 143,229   x   10 6   P a  

E a deformação é dada por: ε x = σ x E =   143,229   x   10 6 200   x   10 9 = 716,15   x   10 - 6 ε y = ε z = - u ε x = - 0,30     x   716,15   x     10 - 6 =   - 214,84   x 10 - 6

Calculando a variação de temperatura quando L = 0,050 m     temos que: a           δ x = L ε x = 0,50   x   716,15   x   10 - 6 = 35,808   x   10 - 6 m

Passo 2

Para Determinarmos a largura da parte AB do corpo de prova, temos que analogamente fazer da mesma maneira que no passo 1, da uma olhadinha, considerando que w = 0,012 m

b           δ y = w ε y = 0,012   x   - 214,84   x   10 - 6 =   - 2,5781   x   10 - 6 m

Passo 3

Para Determinarmos a espessura da parte AB basta aplicarmos na equação abaixo :D

c t = 0,0016 m           δ z = t ε z = 0,0016   x   - 214,84   x       10 - 6 =   - 343,74   x   10 - 9 m

Passo 4

Para Determinarmos a área da seção transversal da parte AB. d A = w 0 1 + ε y   t 0 1 + ε z = w 0 t 0 1 +   ε y + ε z +   ε y   ε z           A 0 = w 0 t 0

∆ A = A - A 0 = w 0 t 0     ε y + ε z + t e r m o   i n s i g n i f i c a n t e = 2 w 0 t 0 ε y

= 2 x   0,012   x   0,0016   x   - 214,84   x   10 - 6 = - 8,25   x   10 - 9 m ²

Resposta

a 0,0358 m m b - 0,00258 m m c - 0,000344 m m d - 0,00825 m m ²  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A placa homogênea ABCD está submetida a um carregamento biaxial como mostra a figura. Sabe-se que σ z = σ 0 e que a variação o comprimento da placa na direção x deve ser zero, ou seja, ϵ x = 0 . Desig
Em muitas situações, sabe-se que a tensão normal em determinada direção é zero, como, σ z = 0 , no caso da placa fina mostrada. Para esse caso, conhecido como estado plano de tensão, mostre que, se as
O bloco plástico mostrado na figura é colado a um suporte rígido e a uma placa vertical à qual é aplicada uma força P de 55kip. Sabendo que, para o plástico utilizado, G = 150k s i determine o desloca
Dois blocos de borracha com um módulo de elasticidade transversal G = 10M P a são colados a dois suportes rígidos e a uma placa A B . Sabendo que b = 200m mec = 125m m , determine a maior força P admi
Um apoio de elastômero ( G = 130p s i ) é utilizado para suportar uma viga mestra de uma ponte, como mostra a figura, para proporcionar flexibilidade durante terremotos. A viga não pode sofrer desloca