Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 72

Para um elemento sob carga axial, expresse a deformação normal ϵ ' em uma direção que forma um ângulo de 45° com o eixo de carga em função da deformação axial ϵ fazendo (a) a comparação da hipotenusa do triangulo mostrado na Fig.2.43, que representa respectivamente o elemento antes e depois da deformação, (b) uso dos valores correspondentes das tensões σ ' e σ s mostrados na Fig 1.38, e alei de Hooke generalizada.

Passo 1

Fala aí gurizada tudo belezinha? O enunciado pede para que a gente faça a comparação da hipotenusa do triangulo do exercício 43. Então vamos desenhar um esboço desse triangulo para realizarmos essa relação, partiu!!!

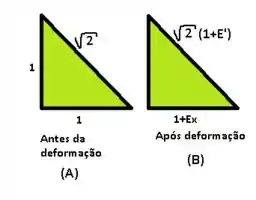
Galera quando falamos em triangulo lembramos do nosso querido Pitágoras então teremos ...

[ 2 1 + ε ' 2 = 1 + ε x 2 + 1 - v ε x 2

2 1 + 2 ε ' + ε ' 2 = 1 + 2 ε x + ε x 2 + 1 - 2 v ε x + v 2 ε x 2 4 ε ' + 2 ε ' 2 = 2 ε x + ε x 2 - 2 v ε x + v 2 ε x 2

Isolando ε ' temos:

ε ' = 1 - v 2 ε x

Passo 2

Vejam abaixo como se comporta as tensões e as deformações até então encontradas...

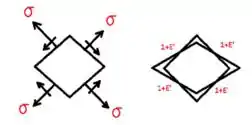
Podemos desconsiderar os valores. 4 ε ' = 2 ε x - 2 v ε x por serem pequenos..

ε ' = σ ' E = v σ ' E

Isolando ε ' temos:

= 1 - v E x P 2 A = 1 - v 2 E σ x ε ' = 1 - v 2 ε x

Resposta

  1. ε ' = 1 - v 2 ε x
  2. ε ' = 1 - v 2 ε x
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um quadrado de 1in, foi riscado na lateral de um grande vaso de pressão. Depois de pressurizado é mostrada a condição de tensão biaxial no quadrado. Sabendo que E = 29x10 6p s i e v = 0,30 , determine
um tecido utilizado em estruturas infláveis está submetido a um carregamento biaxial que resulta em tensões normais σ x = 120M P aeσ y = 160M P a . Sabendo que as propriedades do tecido podem ser de a
Dois blocos de borracha com um módulo de elasticidade transversal G = 12M P a são colados a dois suportes rígidos e a uma placa AB. Sabendo que c = 100m m eP = 45k N , determine as menores dimensões a
As constantes de material E, G, k e v estão relacionadas nas Equações (2.24) e (2.34). mostre que qualquer uma dessas constantes pode ser expressa em função de quaisquer outras duas constantes. Por ex
Para o apoio do elastômero do Problema 2.79 com b = 10 i n . ea = 1 i n . determine o módulo de cisalhamento G e a tensão de cisalhamento τ para uma força lateral máxima P = 5k i p s e um deslocamento