Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 95
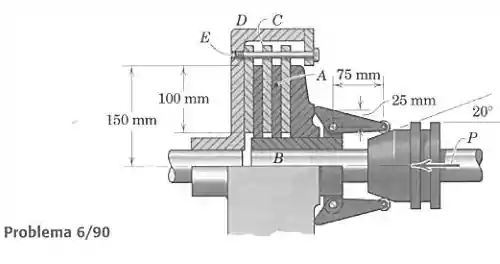
A figura mostra uma transmissão de vários discos projetada para uso marítimo. Os discos de potência são encaixados em uma canaleta no eixo, mas têm que girar com ele. Os discos atuam sobre a estrutura através dos parafusos , ao longo dos quais estão livres para deslizar. Na transmissão mostrada existem cinco pares de superfícies de atrito. Assuma que a pressão está uniformemente distribuída sobre a área dos discos e determine o torque máximo que pode ser transmitido se o coeficiente de atrito vale 0,15 e N.
Passo 1
Primeiro devemos saber qual é a força normal aplicada aos discos por conta da força aplicada ao eixo. Vamos isolar em diagrama de corpo livre a parte onde é aplicada a força e a parte com a roldana que transmite a força aos discos:
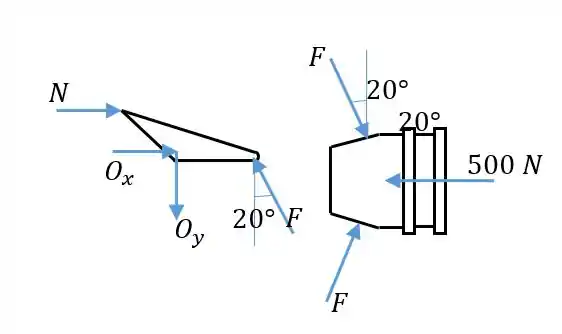
Pela soma das forças horizontais no corpo da direita achamos :
Então fazendo o momento em torno de para o corpo da esquerda determinamos :
Substituindo o valor já achado de , temos:
Passo 2
A fórmula para o momento total causado por um disco de raio maior e raio menor , girando ou na iminêmcia de girar, que sofre uma força normal , com coeficiente de atrito entre as superfícies e pressão uniforme ao longo do disco é:
Temos 5 discos, de raio maior 150 mm e raio menor mm, e a força é a força aplicada em cima e em baixo, igual a:
Então: