Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 122
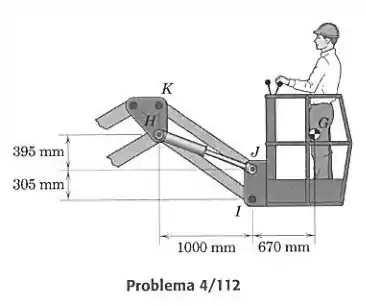
Detalhes adicionais da caçamba do guindaste do Prob. 4/111 estão dados na figura. Determine a força do cilindro devido aos efeitos da massa combinada de 180 kg da caçamba e do operador, com centro de massa em .
Passo 1
Nesse exercício, se formos muito espertos conseguimos calcular a força com uma equação só. Vamos prestar atenção ao desenho, e reparar que e são forças paralelas que atuam no conjunto caçamba-operador. Além dessas duas forças, temos o peso e . Então, se escolhermos um eixo perpendicular a e e fizermos ser zero a soma das forças nessa direção, essas duas forças não aparecem na conta! Teremos apenas e , e aí resolveremos.
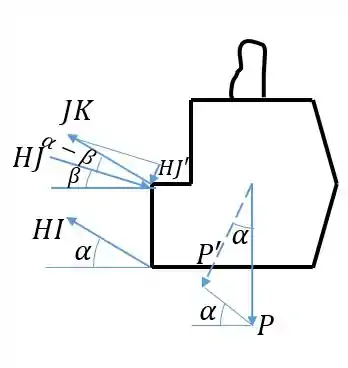
Perceba que se o ângulo entre e a horizontal é e o ângulo entre e a horizontal é , o ângulo entre e é .
Passo 2
Vamos primeiro encontrar os ângulos e , através de suas tangentes:
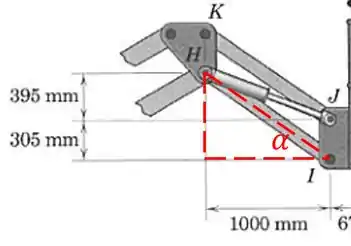
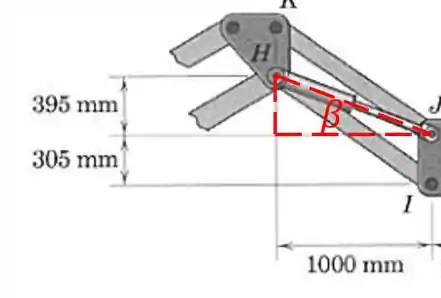
Passo 3
Agora é só somar as forças na direção mostrada:
O sinal negativo indica que erramos no desenho o sentido da força.