Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 111

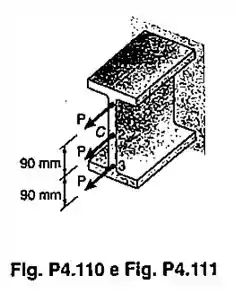
Qualquer dar três cargas axiais, de intensidade P = 45 kN podem ser aplicadas na extremidade de um perfil de aço laminado w200 × 31,3. Determinar a tensão no ponto A: (a) para o carregamento mostrado; (b) se apenas são aplicadas as cargas nos pontos 2 e 3

Passo 1

Para essa questão temos do enunciado

P = 45   k N

O perfile é o W 200 × 31,3 , o que nos dá pelo apêndice

A = 3970   m m 2

I X = 31,3 × 10 6 m m 4 = 31,3 × 10 - 6   m 4

Passo 2

Calculando σ 1  

σ 1 = F A = 3 P A

3P pois temos três forças iguais (P) com mesma direção e sentido.

σ 1 = 3 P A = 3,42 × 10 3 3970 × 10 - 6 = 34,005   M P a

Passo 3

a) Bom, tendo as 3 forças presentes, teremos para o somatório de momentos (sentido horário positivo)

Σ M x = 45 × 90 - 45 × 90 = 0

Para o σ A teremos

σ A = M c I = 0   P a

Então o total é

σ A T O T A L = σ 1 + σ A = 34,005 + 0 = 34,005   M P a

Passo 4

b) Para a letra b nós simplesmente não temos uma das forças. O que isso nos mudo no momento (muita atenção ao sinal!)

Σ M x = - 45 × 90 = - 4,05   k N . m

Para o σ A teremos

σ A = M c I = - 4050 × 10 5 × 10 - 3 31,3 × 10 - 6 = - 13,586   M   P a

Então o total é

σ A T O T A L = 2 × 45 × 10 3 3970 × 10 - 6 + σ A = 22,67 × 10 6 + - 13,586 × 10 6 = 9,084   M P a

Resposta

a ) σ A t o t a l = 34,005   M P a  

b )   σ A t o t a l = 9,084   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a localização do centro de cisalhamento O de viga de paredes finas de espessuras constante que possui a seção transversal mostrada.
Uma viga de paredes finas com espessuras uniforme tem a seção transversal mostrada. Determine a dimensão b de modo que o centro de cisalhamento O da seção transversal fique localizado no ponto indicad
A viga composta mostrada é feita soldando perfis U laminados de aço C 200x17,1 as mesas do perfil de aço laminados de mesas largas W250x80 . Sabendo que a viga é submetida a uma força cortante de 200k
Resolva o Problema 4.150 considerando que o momento M 0 age em um plano horizontal.
Resolva o Problema 4.152 considerando que o momento M 0 atua em um plano horizontal.