Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 29
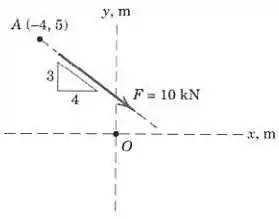
A força de é aplicada no ponto . Calcule o momento de em relação ao ponto . Determine os pontos nos eixos e em relação aos quais o momento de vale zero.
Passo 1
Pessoal, como temos as coordenadas e do ponto , que é o ponto de aplicação da força , será mais simples calcular o momento em relação à origem se decompormos essa força em e , assim:
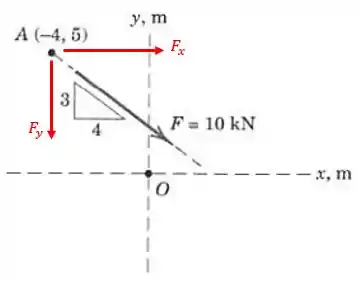
Então, com base no triângulo retângulo pitagórico de lados , e desenhado na figura, considerando como o ângulo adjacente ao cateto , temos os seguintes módulos:
Passo 2
Como a força é aplicada no ponto , a força tende a fazer girar no sentido horário e é aplicada a uma distância vertical de da origem, enquanto tende a fazer girar no sentido anti-horário e é aplicada a uma distância horizontal de da origem.
Então, adotando o sentido anti-horário como positivo, temos:
Ou seja, no sentido horário.
Passo 3
Os pontos nos eixos e em relação aos quais o momento de vale zero pertencem à linha de ação da força, ou seja, temos que achar os pontos de interseção da reta com os eixos e . Da Geometria Analítica, sabemos que a equação da reta vai ser:
Para determinar o coeficiente , substituímos as coordenadas do ponto na equação:
Logo, a equação da reta é
Assim, as interseções com os eixos e serão:
Ou seja, o momento de é nulo em relação aos pontos de coordenadas e , localizados no eixo e no eixo , respectivamente.
Resposta
no sentido horário
e