Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 6.Problemas fundamentais - Ex. 15
Se uma força de é aplicada no cabo do alicate, determine a força de esmagamento exercida sobre o tubo liso e a intensidade da força resultante no pino .
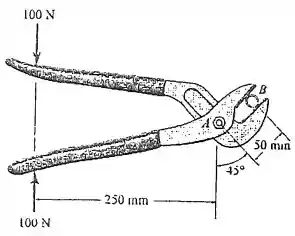
Passo 1
Fala ai galerinha bonita, tudo beleza?
Pra gente determinar a força, devemos fazer o diagrama de corpo livre no qual sejam indicadas todas as forças atuando no alicate. No entanto, como as forças exercidas em cada cabo são iguais, é permitido realizar essa análise em apenas um dos cabos.
Dessa forma, existem a força na ponta do cabo, as reações no pino em e a força de esmagamento em , tal como mostrado no seguinte diagrama:
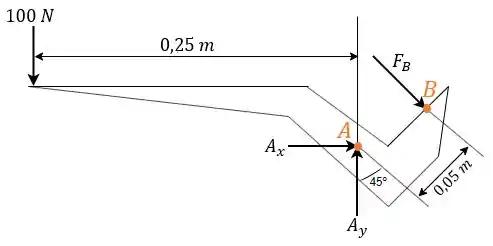
Passo 2
Logo, o princípio dos momentos deve ser aplicado para encontrar a força .
Como existem as reações em sem valor determinado, podemos calcular o momento em relação ao ponto para que, assim, as reações sejam eliminadas durante o cálculo por suas linhas de ação passarem através do ponto de referência. Em outras palavras, isso implicaria em:
E:
Além disso, como as forças em cada cabo atuam em sentidos opostos, o sistema está em equilíbrio e, logo, o momento resultante em cada cabo é nulo.
Deve-se lembrar também que o momento de cada força é dado pelo produto entre a força e sua respectiva distância do ponto de referência até o local de aplicação da força:
Passo 3
Sendo assim, considerando o sentido horário como positivo, o momento das forças em relação ao ponto será dado por:
Passo 4
Agora, para determinar a força resultante em , vamos determinar as componentes horizontal e vertical da reação neste ponto a partir do equilíbrio de forças.
Então, fazendo para o eixo :
Tal que:
Isolando :
E para o eixo :
Substituindo o valores de :
E isolando a reação vertical em :
Portanto, lembrando que a força resultante é função das suas componentes formando um triângulo retângulo, tal que:
A resultante no pino será dada por: