Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 124
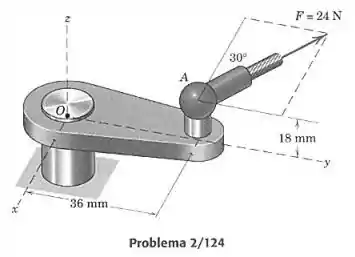
A força de 24 N está aplicada no ponto do conjunto de suportes. Determine o momento dessa força em relação ao ponto .
Passo 1
Podemos calcular o momento causado pela força de duas maneiras: a abordagem vetorial e a abordagem escalar através dos braços de alavanca e usando a regra da mão direita. Vamos calcular através dos braços de alavanca, pois nesse caso é fácil encontrar as componentes de e também as distâncias entre as linhas de aplicação das componentes e o ponto . A força pode ser decomposta em duas componentes, direção e direção . O ângulo entre a direção e a força é de 30°, então:
Por enquando não nos preocupamos com o sinal, pois faremos isso na determinação dos momentos. Calculamos também a componente :
Passo 2
Agora vamos calcular o momento causado em torno de cada direção, , , e . Vamos desenhar as componentes:
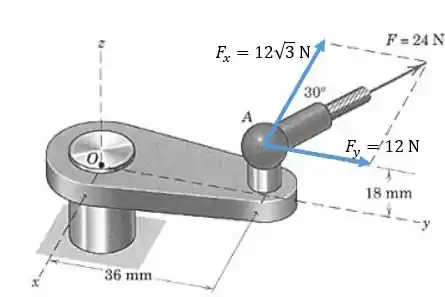
Primeiro vamos calcular o momento em torno da direção . A componente não realiza momento pois é paralela a esse eixo. A distância entre a linha de aplicação de e o eixo é de . Então o módulo do torque é:
Para saber se ele é positivo ou negativo, usamos a regra da mão direita: Esticamos o polegar e fechamos os outros dedos da mão no sentido do giro da força em torno do eixo . É como se fizéssemos um “joinha”. Se o polegar apontar no sentido de , o momento é positivo, se apontar no sentido contrário é negativo.
Fazendo a regra da mão direita para a força em torno do eixo , vemos que o nosso polegar aponta para o sentido contrário de , então o momento é negativo:
Passo 3
Agora já sabemos calcular os momentos nas direções e . Primeiro para a direção , a componente não causa momento pois é paralela ao eixo. A distância entre a linha de ação de e o eixo é também de . Fazendo a regra da mão direita nosso polegar fica apontado no sentido negativo de . Então:
Na direção , somente causa momento, pois a linha de passa em cima do eixo . A distância entre e o eixo é de , e a regra da mão direita indica que o sentido é positivo (polegar fica apontado para cima quando giramos os dedos no sentido do giro de ). Então:
Então multiplicamos as componentes do momento pelos vetores unitários , , e :