Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 3
A força de 300 N é aplicada em A como mostrado na figura. Determine (a) o momento da força de 300 N sobre D, (b) a menor força aplicada em B que cria o mesmo momento em D.
Passo 1
Desenhando o diagrama do corpo livre:
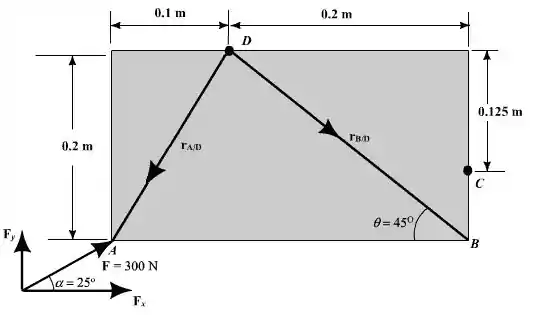
Passo 2
Vamos começar decompondo a força F:
Passo 3
- A partir das componentes, podemos calcular o momento no ponto D pela definição: momento em torno de um ponto é o produto vetorial do braço pela força:
- Do diagrama do corpo livre, vemos que a menor força Q em B tem de ser perpendicular a , o que implica de inclinação. Dessa forma:
Passo 4
Resposta
Exercícios de Livros Relacionados
Parte de um separador mecânico de moedas funciona como se segue: Moedas de um e dez centavos rolam por um plano inclinado de 20 ° , sendo que a parte triangular final do separador gira livremente em r
Ao se levantar o poste a partir da posição mostrada, a força trativa T no cabo deve gerar um momento de 72k N ∙ m em torno de O . Determine T .
Uma força de 200N é aplicada na extremidade da chave de boca para apertar um parafuso que fixa a roda ao eixo. Para a posição mostrada da chave, determine o momento M produzido por esta força em relaç
A plataforma uniforme, que tem uma massa por unidade de comprimento de 28k g / m , está simplesmente apoiada sobre barras de apoio em A e em B . Um trabalhador de construção civil com 90k g sai do pon
Para levantar o mastro O C , uma armação leve O A B é presa ao mastro e uma força trativa de 3,2k N é aplicada ao cabo de sustentação pelo guincho em D . Calcule o momento M O desta força trativa em r